Product: ABAQUS/Standard
The porous elasticity model in ABAQUS/Standard is designed to be used in conjunction with plasticity models that allow plastic volume changes as described in “Models for granular or polymer behavior,” Section 4.4.2, to “Models for crushable foams,” Section 4.4.6. Use of the porous elasticity model without one of these plasticity options is not recommended. The model is based on the experimental observation that in porous materials during elastic (recoverable) straining, the change in the void ratio—e—and the change in the logarithm of the equivalent pressure stress—p—defined as
is a material parameter. In this form the material has zero tensile strength. If the tensile strength 
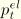
is nonzero, the equivalent relation is which includes the special case of zero tensile strength (
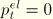
). It can be shown that, if the compressibility of the solid material is neglected, the volume change of a material sample is where 
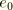
is the initial void ratio. If we define the elastic void ratio from the elastic volume change according to the relationship and then integrate the linear relation, the volumetric elasticity relationship is where 
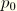
is the initial pressure stress, prescribed by initial conditions. Note that for a zero tensile strength material it is required that 
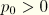
. This equation can be inverted to yield as illustrated in Figure 4.4.1–1.The deviatoric elastic behavior is defined either by choosing a constant shear modulus, G, so that the deviatoric elastic stiffness is independent of the equivalent pressure stress or choosing a constant Poisson's ratio, 
, so that the deviatoric elastic stiffness increases as the equivalent pressure stress increases. If a constant shear modulus is given, the deviatoric relationship is
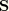
is the deviatoric stress: 
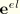
is the deviatoric part of the elastic strain: 
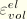
is the volumetric part of the elastic strain.
