
Products: ABAQUS/Standard ABAQUS/Explicit
ABAQUS includes a family of elements that can be used to represent fluid-filled cavities under hydrostatic conditions. These elements provide the coupling between the deformation of the fluid-filled structure and the pressure exerted by the contained fluid on the boundary of the cavity. In ABAQUS/Explicit the fluid must be compressible and the pressure is calculated from the cavity volume. In ABAQUS/Standard the fluid inside the cavity can be compressible or incompressible, with the fluid volume given as a function of the fluid pressure, p; the fluid temperature, ![]() ; and the fluid mass, m, in the cavity:
; and the fluid mass, m, in the cavity:
![]()
![]()
![]()
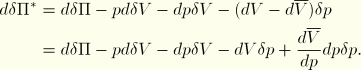
Since the pressure is the same for all elements in the cavity, the augmented virtual work expression can be written as the sum of the expressions for the individual elements:
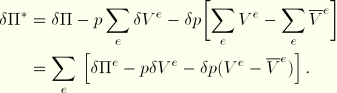
![]()
![]()

In ABAQUS/Standard the fluid is incompressible by default and the fluid volume, ![]() , is dependent upon temperature but independent of the fluid pressure:
, is dependent upon temperature but independent of the fluid pressure:
![]()
![]()
The total fluid mass in the cavity is the sum of the fluid masses of the elements making up the cavity:
![]()
![]()
![]()
The fluid density at the current pressure and temperature, ![]() , is obtained as
, is obtained as
![]()
Thus, the fluid volume at the current pressure and temperature is
![]()
![]()
Fluid can be added to or removed from the cavity. The amount of fluid added is given as the change in (fluid) mass ![]() . Consequently, the change of the fluid volume at the current cavity temperature is
. Consequently, the change of the fluid volume at the current cavity temperature is
![]()

In this case the fluid is compressible, and the volume is a function of the pressure and the temperature in the cavity:
![]()
![]()
![]()
![]()
![]()

The hydrostatic fluid elements appear as surface elements that cover the cavity boundary, but they are actually volume elements when the cavity reference node is accounted for. Figure 3.8.1–1 depicts the 4-node hydrostatic fluid volume element, F3D4. The dashed lines indicate that the element is actually pyramidal in shape.
The volume, ![]() , of each element must be calculated. The coordinates of any point on the base of the pyramid element can be found by
, of each element must be calculated. The coordinates of any point on the base of the pyramid element can be found by
![]()
![]()
![]()
![]()
![]()
![]()
![]()
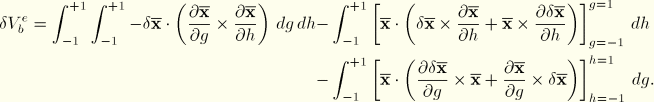
![]()
The second variation of the expression for the volume is
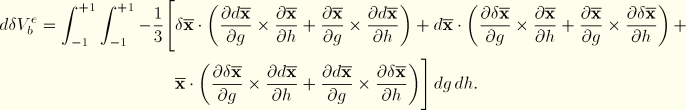
![]()
![]()
The integrations can be carried out analytically. For instance, for element type F3D4 the above expressions yield, after some manipulation,
![]()
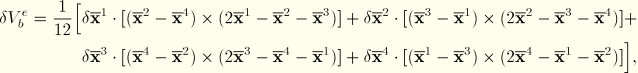
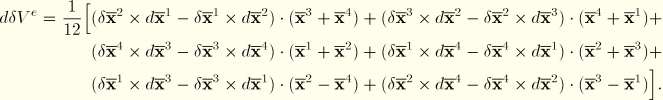

In addition to the fluid cavity elements ABAQUS also offers a 2-node fluid link element that can be used to model fluid flow between two cavities or between a cavity and the outside world. This is typically used when the fluid has to flow through a narrow orifice. It is assumed that the mass flow rate, q, through the link is a homogeneous function of the pressure difference, ![]() . In addition, it is assumed that the flow rate may depend on the average temperature—
. In addition, it is assumed that the flow rate may depend on the average temperature—![]() —and, for a compressible fluid, on the average pressure—
—and, for a compressible fluid, on the average pressure—![]() :
:
The flow rate needs to be integrated over a finite increment. We assume that the dependence on the average pressure, ![]() , is weak. Hence, we use a semi-implicit method: we use
, is weak. Hence, we use a semi-implicit method: we use ![]() at the end of the increment and
at the end of the increment and ![]() at the start of the increment. For the temperature we choose
at the start of the increment. For the temperature we choose ![]() to be the average of
to be the average of ![]() at the start and end of the increment, because this is likely to be the most accurate. Hence, we obtain the mass flow through the link:
at the start and end of the increment, because this is likely to be the most accurate. Hence, we obtain the mass flow through the link:
![]()
This mass change needs to be converted to a volume change in each cavity. It is assumed that the fluid in both cavities is the same, but the pressures (and possibly the temperatures) may be different. With use of the pressure and temperature-dependent density ![]() for each cavity i, the relations become
for each cavity i, the relations become
![]()
Many applications of fluid flow through a fluid link involve dynamic loading in the form of steady-state vibration; and often in such cases the dissipative losses in the fluid link must be modeled to obtain useful results. In most problems of this class the fluids on either side of the fluid link are first pressurized statically. In the implementation in ABAQUS/Standard, it is assumed that the vibration amplitude is sufficiently small that the fluid link response in the dynamic phase of the problem can be treated as linear perturbations about the prepressurized state.
For small vibrations about a prepressurized state we linearize Equation 3.8.1–1 to give
![]()
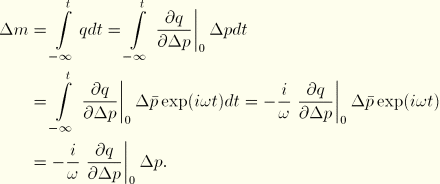
Substituting the above expression for mass flow into Equation 3.8.1–2 and noting that ![]() yields
yields
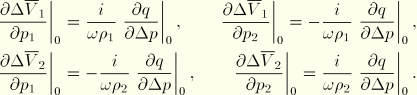
In ABAQUS this model is provided only for the direct-solution steady-state dynamic analysis procedure.

It is possible that negative eigenvalues will be encountered in the solution of certain hydrostatic fluid element problems. With standard elements this can indicate that a bifurcation or buckling load has been exceeded. However, this is not necessarily true with hydrostatic fluid elements; negative eigenvalues can result solely from the numerical implementation.
Consider the simple hydrostatic fluid model depicted in Figure 3.8.1–2.
If the fluid is considered incompressible, application of the downward force causes the fluid to compress vertically and expand horizontally, while maintaining the original fluid volume. Thus, the model can be adequately discretized as a three degree of freedom system: the horizontal displacement of the right platen, u; the vertical displacement of the top platen, v; and the fluid pressure, p. The corresponding system of equations in matrix form is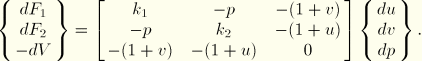
The equation solver processes the equations in sequence. Hence, it will process the ![]() submatrix relating the displacements to the forces prior to processing the constraints. This leads to a negative eigenvalue if
submatrix relating the displacements to the forces prior to processing the constraints. This leads to a negative eigenvalue if ![]() . However since the mode associated with the negative eigenvalue is subsequently constrained by the continuity equation, no instability occurs.
. However since the mode associated with the negative eigenvalue is subsequently constrained by the continuity equation, no instability occurs.