All the solid elements in ABAQUS allow for finite strain and rotation in large-displacement analysis. For kinematically linear analysis the strain is defined as

where is the total displacement and is the spatial position of the point under consideration in the original configuration. As discussed in Chapter 1, “Introduction and Basic Equations,” this measure of strain is useful only if the strains and rotations are small (all components of the strain and rotation matrices are negligible compared to unity).

For cases where the strains and/or rotations are no longer small, two ways of measuring strain are used in the solid elements in ABAQUS. When the hyperelastic or hyperfoam material definition is used with an element, ABAQUS internally uses the stretch values calculated directly from the deformation gradient matrix, , to compute the material behavior. With any other material behavior it is assumed that any elastic strains are small compared to unity, so the appropriate reference configuration for the elasticity is only infinitesimally different from the current configuration and the appropriate stress measure is, therefore, the Cauchy (“true”) stress. (More precisely, the appropriate stress measure should be the Kirchhoff stress defined with respect to the elastic reference configuration, but the assumption that this reference configuration and the current configuration are only infinitesimally different makes the Kirchhoff and Cauchy stress measures almost the same: the differences are on the order of the elastic strains compared to unity). The conjugate strain rate to Cauchy stress is the rate of deformation,

where is the velocity at a point and are the current spatial coordinates of the point. The strain is, therefore, defined as the integral of the rate of deformation. This integration is nontrivial, particularly in the general case where the principal axes of strain rotate during the deformation. In ABAQUS the total strain is constructed by integrating the strain rate approximately over the increment by the central difference algorithm; and, when the strain components are referred to a fixed coordinate basis, the strain at the start of the increment must also be rotated to account for the rigid body rotation that occurs in the increment. This is also done approximately, using the Hughes-Winget (1980) method. This integration algorithm defines the integration of a tensor associated with the material behavior as where is the tensor; is the increment in the tensor associated with the material's constitutive behavior, and, therefore, dependent on the strain increment, , defined by the central difference formula as where ; and is the increment in rotation, defined by Hughes and Winget as where is the central difference integration of the rate of spin: A somewhat different algorithm to calculate is used for the Green-Naghdi rate in ABAQUS/Explicit.

For example, the stress is integrated by this method as

where is the stress increment caused by the straining of the material during this time increment and is the Kirchhoff ( Cauchy) stress. The subscripts t and refer to the beginning and the end of the increment, respectively.

As shown in “Procedures: overview and basic equations,” Section 2.1.1, the contribution of the internal work terms to the Jacobian of the Newton method that is often used in ABAQUS/Standard is

where and are evaluated at the end of the increment.

Using the integration definition above, it can be shown that

where is the Jacobian matrix of the constitutive model:

However, rather than computing the tangent matrix for the Newton method on this basis, we approximate this by using

which yields the Jacobian

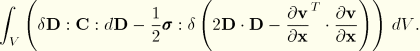
This Jacobian is the tangent stiffness of the rate form of the problem. Experience with practical cases suggests that this approximation provides an acceptable rate of convergence in the Newton iterations in most applications with real materials.

The strain and rotation measures described above are approximations. Probably the most limiting aspect of these approximations is the definition of the rotation increment . While this measure does give a representation of the rotation of the material at a point in some average sense (both in ABAQUS/Standard and ABAQUS/Explicit), it is clear that each of the individual material fibers at a point has a different rotation (unless the material point undergoes rigid body motion only or, as an approximate extension, if the strains at the point are small). This suggests that the formulation described above will not be suitable for applications where the strains and rotations are large and where the material exhibits some form of anisotropic behavior. A common example of such cases is the induction of anisotropy through straining, as in “kinematic hardening” plasticity models. The integration methods described above are not suitable for such material models at large strains (for practical purposes with typical material parameters this means that the solutions will be quite wrong when the strains are greater than 20%–30%). Therefore, the use of the kinematic hardening model in ABAQUS at such strain levels is not recommended. There is extensive literature on this subject; for example, see Agah-Tehrani et al. (1986).