
Product: ABAQUS/Standard
The basic substructuring idea is to consider a “substructure” (a part of the model) separately and eliminate all but the degrees of freedom needed to connect this part to the rest of the model so that the substructure appears in the model as a “substructure”: a collection of finite elements whose response is defined by the stiffness (and mass) of these retained degrees of freedom denoted by the vector, ![]() .
.
In ABAQUS/Standard the response within a substructure, once it has been reduced to a substructure, is considered to be a linear perturbation about the state of the substructure at the time it is made into a substructure. Thus, the substructure is in equilibrium with stresses ![]() , displacements
, displacements ![]() , and other state variables
, and other state variables ![]() when it is made into a substructure. Then, whenever it responds as a substructure, the total value of a displacement or stress component at some point within the substructure is
when it is made into a substructure. Then, whenever it responds as a substructure, the total value of a displacement or stress component at some point within the substructure is
![]()
![]()
The reduced stiffness matrix is easily derived when only static response is considered. Since the response of a substructure is entirely linear, its contribution to the virtual work equation for the model of which it is a part is
![]()
![]()
Since the internal degrees of freedom in the substructure, ![]() , appear only within the substructure, the equilibrium equations conjugate to
, appear only within the substructure, the equilibrium equations conjugate to ![]() in the contribution to the virtual work equation given above are complete within the substructure, so that
in the contribution to the virtual work equation given above are complete within the substructure, so that
![]()
![]()
![]()
![]()
The static modes defined by Equation 2.14.1–1 may not be sufficient to define the dynamic response of the substructure accurately. The substructure's dynamic representation may be improved by retaining additional degrees of freedom not required to connect the substructure to the rest of the model; that is, some of the ![]() can be moved into
can be moved into ![]() . This technique is known as Guyan reduction. An additional, and generally more effective, technique is to augment the response within the substructure by including some generalized degrees of freedom,
. This technique is known as Guyan reduction. An additional, and generally more effective, technique is to augment the response within the substructure by including some generalized degrees of freedom, ![]() , associated with natural modes of the substructure. The simplest such approach is to extract some natural modes from the substructure with all retained degrees of freedom constrained, so that Equation 2.14.1–1 is augmented to be
, associated with natural modes of the substructure. The simplest such approach is to extract some natural modes from the substructure with all retained degrees of freedom constrained, so that Equation 2.14.1–1 is augmented to be
![]()
![]()
![]()
The contribution of the substructure to the virtual work equation for the dynamic case is
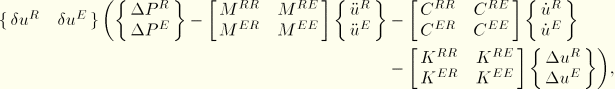
![]()
![]()
![]()
With the assumed dynamic response within the substructure, the internal degrees of freedom in this contribution (![]() and its time derivatives) can be transformed to the retained degrees of freedom and the normal mode amplitudes, reducing the system to
and its time derivatives) can be transformed to the retained degrees of freedom and the normal mode amplitudes, reducing the system to
![]()
![]()

Large-rotation substructures require first the computation of an equivalent rigid body rotation matrix ![]() associated with the substructure's motion. Since the substructure exhibits only small deformations, one can use the original and current positions of two nodes in two-dimensional analyses or three nodes in three-dimensional analyses to compute two rectangular local systems and then the rotation matrix. For example, in three dimensions ABAQUS/Standard computes a reference (average) point using the three nodes in the original configuration. The first unit direction vector,
associated with the substructure's motion. Since the substructure exhibits only small deformations, one can use the original and current positions of two nodes in two-dimensional analyses or three nodes in three-dimensional analyses to compute two rectangular local systems and then the rotation matrix. For example, in three dimensions ABAQUS/Standard computes a reference (average) point using the three nodes in the original configuration. The first unit direction vector, ![]() , points from this average point to the first node. The third direction,
, points from this average point to the first node. The third direction, ![]() , is taken to be the normal to the plane defined by the three nodes and the second direction,
, is taken to be the normal to the plane defined by the three nodes and the second direction, ![]() , is simply the cross-product of the third and first directions. The process is repeated in the current configuration to compute a local system,
, is simply the cross-product of the third and first directions. The process is repeated in the current configuration to compute a local system, ![]() . The rotation matrix can then be easily computed as
. The rotation matrix can then be easily computed as ![]() .
.
ABAQUS/Standard automatically picks the two or three nodes used for the computation of the rotation matrix ![]() from the substructure's retained nodes. In most cases only retained nodes with at least all translational degrees of freedom retained can be canditates. For example, in three-dimensional analyses the first node used for the equivalent rigid body calculation is chosen to be the node with the highest stiffness (largest diagonal value) in the substructure. The second node is chosen to be the retained node farthest apart from the first node with the provision that its nodal stiffness is high enough (at least 0.01% of the stiffness of the first node). The third node is picked to be the retained node for which the distance to the line defined by the first and second node is maximum (with the same stiffness requirement as for the second node). In the rare case when less than three (in three-dimensional analyses) valid candidate nodes are retained, the
from the substructure's retained nodes. In most cases only retained nodes with at least all translational degrees of freedom retained can be canditates. For example, in three-dimensional analyses the first node used for the equivalent rigid body calculation is chosen to be the node with the highest stiffness (largest diagonal value) in the substructure. The second node is chosen to be the retained node farthest apart from the first node with the provision that its nodal stiffness is high enough (at least 0.01% of the stiffness of the first node). The third node is picked to be the retained node for which the distance to the line defined by the first and second node is maximum (with the same stiffness requirement as for the second node). In the rare case when less than three (in three-dimensional analyses) valid candidate nodes are retained, the ![]() matrix is computed directly from the nodal rotations of the stiffest node with all rotational degrees of freedom retained.
matrix is computed directly from the nodal rotations of the stiffest node with all rotational degrees of freedom retained.
To compute internal forces associated with a substructure in large rotations, ABAQUS/Standard computes strain-inducing displacements/rotations by “subtracting” the rigid body motion from the substructure's nodal displacements/rotations. For translational degrees of freedom the strain-inducing displacements ![]() at a node can be computed using
at a node can be computed using
![]()
![]()
![]()
![]()
![]()
Similarly, in dynamics the reduced mass (including the coupling between nodal displacements/rotations and eigenmode contributions) is rigid body rotated before any mass contributions are included in the virtual work associated with the substructure.

When gravity loading that acts in a fixed direction is defined, ABAQUS/Standard will create internally at the generation level a number of load cases (two in two-dimensional analyses and three in three-dimensional analyses) corresponding to unit gravity loads in the substructure's directions. At the usage level the total rotation matrix of the substructure ![]() (includes both the user-specified rotation/mirroring and the rotation of the substructure in nonlinear geometry analyses) is first used to rotate back the user-specified unit direction
(includes both the user-specified rotation/mirroring and the rotation of the substructure in nonlinear geometry analyses) is first used to rotate back the user-specified unit direction ![]() for the gravity load. Thus, the user-specified directions are now expressed in the local (rotating) system associated with the substructure (
for the gravity load. Thus, the user-specified directions are now expressed in the local (rotating) system associated with the substructure (![]() ). The internally generated unit load cases are then scaled by the components of
). The internally generated unit load cases are then scaled by the components of ![]() and by the appropriate magnitude and amplitude and then added to the external force in the model.
and by the appropriate magnitude and amplitude and then added to the external force in the model.