For the liquid in the system (the free liquid in the voids and the entrapped liquid) we assume that

where is the density of the liquid, is its density in the reference configuration, is the liquid's bulk modulus, and is the volumetric expansion of the liquid caused by temperature change. Here is the liquid's thermal expansion coefficient, is the current temperature, is the initial temperature at this point in the medium, and is the reference temperature for thermal expansion. Both and are assumed to be small.

The solid matter in the porous medium is assumed to have the local mechanical response under pressure

where is the bulk modulus of this solid matter, s is the saturation in the wetting fluid, and is its volumetric thermal strain. Here is the thermal expansion coefficient for the solid matter and is the reference temperature for this expansion. is assumed to be small.

It is important to distinguish and as properties of the solid grains material. The porous medium as a whole will exhibit a much softer (and generally nonrecoverable) bulk behavior than is indicated by and will also show a different thermal expansion. These effects are partially structural, caused by the medium being made up of irregular grains in partial contact. They may also be caused by the system being only partially saturated, with the voids containing a mixture of relatively compressible gas and relatively incompressible liquid.

Entrapment of liquid is associated with specific materials that absorb liquid and swell into a “gel.” A simple model of this behavior is based on the idealization of this gel as a volume of individual spherical particles of equal radius . Tanaka and Fillmore (1979) show that, when a single sphere of such material is fully exposed to liquid, its radius change can be modeled as

where is the fully swollen radius approached as and N, and are material parameters. Tanaka and Fillmore also show the first term in the series dominates, so the model can be simplified to This provides the rate form

When the gel particles are only partially exposed to liquid (in an unsaturated system), it seems reasonable to assume that the swelling rate will be lessened according to the level of saturation. Further, we assume that the gel will swell only when the saturation of the surrounding medium exceeds the effective saturation of the gel, , where is the radius of a gel particle that is completely dry. We combine these into a simple, linear effect:

where if , otherwise.

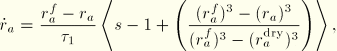
The packing density and swelling may cause the gel particles to touch. In that case the surface available to absorb and entrap liquid is reduced until, if the gel particles occupy the entire volume except for solid material, liquid entrapment must cease altogether. With gel particles per unit reference volume, the maximum radius that the gel particles can achieve before they must touch (in a face center cubic arrangement) is

and the volume is entirely occupied with gel and solid matter when the effective gel radius is The gel swelling behavior is, therefore, further modified to be Thus, in an unstressed medium the entrapped liquid volume is assumed to be where where is defined by the integration of Equation 2.8.3–3. This entrapped liquid can be compressed by pressure so that, when the porous medium is under stress, we assume and thus Combining this with Equation 2.8.3–1 and neglecting small terms compared to unity then provides

We assume that, in the initial state, the effective saturation of the gel is the same as the saturation of the surrounding medium:

The constitutive behavior of the gel containing entrapped fluid is given by the elastic bulk relationship

where is the average pressure stress in the gel fluid and is its volumetric effective strain.

From Equation 2.8.3–2 we see that the volumetric strain represents that part of the total volumetric strain caused by pore pressure acting on the solid matter in the porous medium and by thermal expansion of that solid matter. In addition, entrapment of liquid in the medium may cause an additional volume change ratio:

Finally, is a saturation driven moisture swelling strain that represents the volumetric swelling of the solid skeleton in partially saturated flow conditions. This moisture swelling can be isotropic or anisotropic. The remaining part of the strain in the medium, is the strain that is assumed to modify the effective stress in the medium. That is, we assume Specific constitutive models of this type are discussed in Chapter 4, “Mechanical Constitutive Theories.” From this assumption, and using Equation 2.8.3–5, we can write the Jaumann rate of change of the effective stress in terms of the rate of change of the kinematic and pore liquid pressure variables as where is defined for each particular model in Chapter 4, “Mechanical Constitutive Theories.”

Also, for the effective pressure stress of the fluid entrapped in the gel,

Then, from Equation 2.8.2–3,