The stress-strain behavior of typical rubber materials, which is shown in Figure 5–25, is elastic but highly nonlinear.
This type of material behavior is called hyperelasticity. The deformation of hyperelastic materials, such as rubber, remains elastic up to large strain values (often well over 100%).ABAQUS/Explicit makes the following assumptions when modeling a hyperelastic material:
The material behavior is elastic.
The material behavior is isotropic.
The material is nearly incompressible (Poisson's ratio is 0.475 by default.)
Elastomeric foams are another class of highly nonlinear, elastic materials. They differ from rubber materials in that they have a highly compressible behavior when subjected to compressive loads. They are modeled using the hyperfoam model in ABAQUS/Explicit. The hyperfoam model will not be discussed in this guide.
ABAQUS uses a strain energy potential (U), rather than a Young's modulus and Poisson's ratio, to relate stresses to strains in hyperelastic materials. Several different strain energy potentials are available: a polynomial model, the Ogden model, the Arruda-Boyce model, and the van der Waals model. Simpler forms of the polynomial model are also available, including the Mooney-Rivlin, neo-Hookean, reduced polynomial, and Yeoh models.
The polynomial form of the strain energy potential is the one that is most commonly used. Its form is
is the strain energy potential; 
is the elastic volume ratio; 
and 
are measures of the distortion in the material; and 
, 
, and 
are material parameters, which may be functions of temperature. The parameters describe the shear behavior of the material, and the parameters introduce compressibility. If the material were fully incompressible (a condition not allowed in ABAQUS/Explicit), all the values of would be zero, and the second part of the equation shown above could be ignored. If the number of terms, , is one, the initial shear modulus, 
, and bulk modulus, 
, are given by
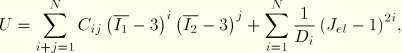
The other hyperelastic material models are similar in concept and are described in the ABAQUS Analysis User's Manual.
You must provide ABAQUS with the relevant material parameters to use a hyperelastic material. For the polynomial form these are , , and . It is possible that you will be supplied with these parameters when modeling hyperelastic materials; however, more likely you will be given test data for the materials that you must model. ABAQUS can accept test data directly and calculate the material parameters for you (using a least squares fit).
A convenient way of defining a hyperelastic material is to supply ABAQUS with experimental test data. ABAQUS then calculates the constants using a least squares method. The experimental tests for which ABAQUS can fit data are:
Uniaxial tension and compression.
Equibiaxial tension and compression.
Planar tension and compression (pure shear).
Volumetric tension and compression.
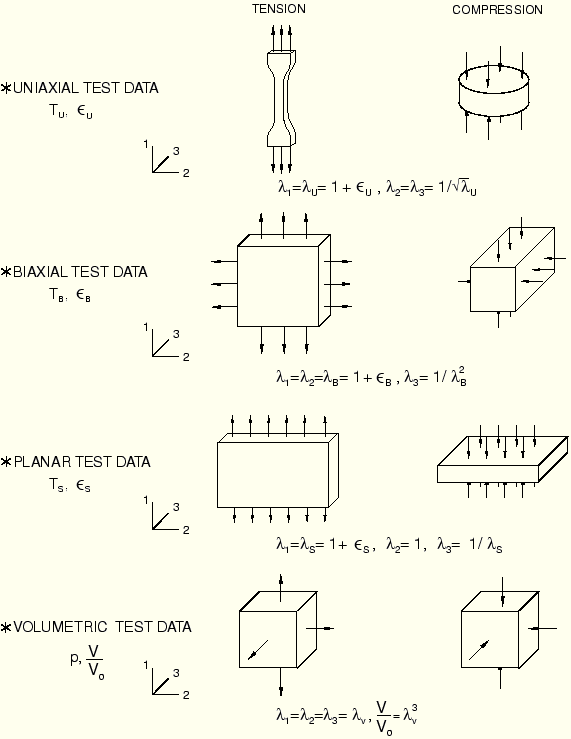
The deformation modes seen in these tests and the ABAQUS input options used to define the data for each are shown in Figure 5–26. Unlike plasticity data, the test data for hyperelastic materials must be given to ABAQUS as nominal stress and nominal strain values.
Figure 5–26 Deformation modes and ABAQUS input options for the various experimental tests for defining hyperelastic material behavior.
Achieving the best material model from your data
The quality of the results from a simulation using hyperelastic materials strongly depends on the material test data that you provide ABAQUS. There are several things that you can do to help ABAQUS calculate the best possible material parameters.
Wherever possible, try to obtain experimental test data from more than one deformation state to help ABAQUS form a much more accurate and stable material model. Some of the tests shown in Figure 5–26 produce equivalent deformation modes for incompressible materials. The following are equivalent tests for incompressible materials:
Uniaxial tension ↔ Equibiaxial compression.
Uniaxial compression ↔ Equibiaxial tension.
Planar tension ↔ Planar compression.
In addition, the following may improve your hyperelastic material model:
Obtain test data for the deformation modes that are likely to occur in your simulation. For example, if your component is loaded in compression, make sure that your test data include compressive, rather than tensile, loading.
Both tension and compression data are allowed, with compressive stresses and strains entered as negative values. If possible, use compression or tension data depending on the application, since the fit of a single material model to both tensile and compressive data will normally be less accurate for each individual test.
Provide more data at the strain magnitudes that you expect the material will be subjected to during the simulation. For example, if the material will only have small tensile strains, say under 50%, do not provide much, if any, test data at high strain values (over 100%).
Perform one-element simulations of the experimental tests, and compare the results ABAQUS calculates to the experimental data. If the computational results are poor for a particular deformation mode that is important to you, try to obtain more experimental data for that deformation mode.
These one-element simulations are very easy to perform in ABAQUS/CAE. Please consult the ABAQUS/CAE User's Manual for details.
Stability of the material model
It is possible for the hyperelastic material model determined from the test data to be unstable at certain strain magnitudes. ABAQUS performs a stability check to determine the strain magnitudes where unstable behavior will occur and prints a warning message in the data (.dat) file. You should check this information carefully since your simulation may not be realistic if any part of the model experiences strains beyond the stability limits.
See “Hyperelastic behavior of rubberlike materials,” Section 17.5.1 of the ABAQUS Analysis User's Manual, for suggestions on improving the accuracy and stability of the test data fit.
Compressibility
Most solid rubber materials have very little compressibility compared to their shear flexibility. This behavior is not a problem with plane stress, shell, or membrane elements. However, it can be a problem when using other elements, such as plane strain, axisymmetric, and three-dimensional solid elements. For example, in applications where the material is not highly confined, it would be quite satisfactory to assume that the material is fully incompressible: the volume of the material cannot change except for thermal expansion. In cases where the material is highly confined (such as an O-ring used as a seal), the compressibility must be modeled correctly to obtain accurate results.
Except for plane stress cases, it is not possible to assume that the material is fully incompressible in ABAQUS/Explicit because the program has no mechanism for imposing such a constraint at each material calculation point. An incompressible material also has an infinite wave speed, resulting in a time step of zero. Therefore, you must provide some compressibility. The difficulty is that, in many cases, the actual material behavior provides too little compressibility for the algorithms to work efficiently. Thus, except for plane stress, the user must provide enough compressibility for an efficient solution, knowing that this makes the bulk behavior of the model softer than that of the actual material. Therefore, some judgement is required to decide whether or not the solution is sufficiently accurate or whether the problem can be modeled at all with ABAQUS/Explicit because of this numerical limitation. We can assess the relative compressibility of a material by the ratio of its initial bulk modulus, , to its initial shear modulus, . Poisson's ratio, 
, also provides a measure of compressibility since it is defined as
Table 5–2 provides some representative values:
Table 5–2 Relationship between compressibility and Poisson's ratio.
 | Poisson's ratio |
|---|---|
| 10 | 0.452 |
| 20 | 0.475 |
| 50 | 0.490 |
| 100 | 0.495 |
| 1,000 | 0.4995 |
| 10,000 | 0.49995 |
If no value is given for the material compressibility in the hyperelastic option, by default ABAQUS/Explicit assumes 
, corresponding to a Poisson's ratio of 0.475. Since typical unfilled elastomers have 
ratios in the range of 1,000 to 10,000 (
0.4995 to 0.49995) and filled elastomers have ratios in the range of 50 to 200 ( 0.490 to 0.497), this default provides much more compressibility than is available in most elastomers. However, if the elastomer is relatively unconfined, this softer modeling of the material's bulk behavior usually provides quite accurate results. However, in cases where the material is highly confined—such as when it is in contact with stiff, metal parts and has a very small amount of free surface, especially when the loading is highly compressive—it may not be feasible to obtain accurate results with ABAQUS/Explicit.
If you are defining the compressibility rather than accepting the default value, an upper limit of 100 is suggested for the ratio of . Larger ratios introduce high-frequency noise into the dynamic solution and require the use of excessively small time increments.
