Product: ABAQUS/Explicit
This example problem demonstrates the following ABAQUS features and techniques:
using ductile, shear, and Müschenborn-Sonne forming limit diagram (MSFLD) damage initiation criteria to study the initiation of failure due to three different mechanisms: ductile fracture, shear band formation, and necking instability, respectively; and
modeling progressive failure of components using damage evolution and element removal.
New materials such as aluminum and magnesium alloys and high-strength steels are being introduced increasingly in automotive components to reduce weight and, hence, to increase overall vehicle performance. These materials typically have low ductility at fracture compared to traditional steels and may suffer damage and failure under crash loading conditions. A typical component made of sheet metal may undergo damage due to a number of mechanisms including void nucleation and coalescence, shear band formation, and necking instability. Thus, to obtain reliable predictions from crashworthiness simulations, it is essential to model damage initiation and progressive failure due to various failure mechanisms as well as modeling accurate plastic deformation behavior. In this example problem we consider the overall deformation and failure behavior of a thin-wall, double-chambered aluminum extrusion under quasi-static three-point bending and dynamic axial loading conditions. The overall load-displacement response and the fracture patterns are compared with the experimental results given by Hooputra et al. (2004).
The three-point bending and the axial crushing configurations are shown in Figure 2.1.16–1 and Figure 2.1.16–6, respectively. The overall dimensions of the aluminum extrusion are L=500 mm, W=95 mm, and H=68 mm for the three-point bending case and L≈396.5 mm, W=95 mm, and H=68 mm for the axial crushing case. The thickness of the sheet is 2.5 mm for both cases.
The material used in this study is an extruded aluminum alloy EN AW-7108 T6. This material behaves in an elastic-plastic manner and can undergo damage due to either one or a combination of the following damage mechanisms: nucleation and coalescence of voids, shear band formation, and necking instability.
The three-point bending configuration consists of the aluminum extrusion supported on two rigid cylinders and loaded in the transverse direction by another rigid cylinder (Figure 2.1.16–1). In the axial crushing simulation, one end of the aluminum extrusion is supported by a fixed rigid base and the other end is subjected to an instantaneous velocity by a planar rigid impactor (Figure 2.1.16–6).
Two loading cases are considered. The first case consists of a quasi-static three-point bending configuration where the part is loaded transversely to the extrusion direction. In the second case the part is subjected to a dynamic loading in the axial (extrusion) direction.
The sections that follow discuss the analysis considerations that are applicable to both cases.
In both cases the mesh is similar to that used by Hooputra et al. (2004). The aluminum extrusion is meshed with a uniform mesh consisting primarily of 4-node shell elements (S4R). In the axial crushing case some 3-node shell elements (S3R) are also used. The planar dimensions of the elements are an order of magnitude larger than the shell thickness. The simulations with this mesh yield results in agreement with the experimental observations. No mesh refinement studies were conducted.
The details of the ABAQUS models used for constitutive behavior and progressive damage analysis are discussed below. Guidelines for obtaining the material parameters from experimental data are also provided.
Hooputra et al. (2004) have shown that the extruded aluminum alloy EN AW-7108 T6 displays plastic orthotropy due to the nature of the extrusion processing and have used the Barlat symmetric yield locus (Barlat et al., 1991) to fit the experimental data. In this example we neglect the orthotropy and assume both the elastic and the plastic behavior to be isotropic with the yield surface described by the Mises yield function (see “Inelastic behavior,” Section 18.1.1 of the ABAQUS Analysis User's Manual). The assumption of isotropic plasticity may appear to be too restrictive for the accurate prediction of failure in extruded alloys. However, in crashworthiness simulations the assumption of isotropy usually yields acceptable results when compared with experimental observations, as shown in the results obtained in this example. Nevertheless, you should compare your simulation results with experimental data to check the validity of the isotropic plasticity assumption.
Metal sheets and thin-walled extrusions made of aluminum alloys may fail due to one or a combination of the following failure mechanisms (Hooputra et al. 2004): ductile failure due to nucleation, growth, and coalescence of voids; shear failure due to fracture within shear bands; and failure due to necking instabilities. If the model consists of shell elements, a criterion for the last failure mechanism is necessary because the size of the localized neck is of the order of the sheet thickness and, hence, cannot be resolved with shell elements of dimensions one order of magnitude larger than the thickness.
ABAQUS/Explicit offers a number of damage initiation criteria to model the onset of necking instabilities in sheet metals. These include the Forming Limit Diagram (FLD), Forming Limit Stress Diagram (FLSD), Müschenborn-Sonne Forming Limit Diagram (MSFLD), and Marciniak-Kuczynski (M-K) criteria. The first three criteria utilize the experimentally measured forming limit curves in the appropriate strain or stress spaces. The last criterion introduces virtual thickness imperfections in the sheet metal and analyzes the deformation in the imperfection zone to determine the onset of the instability (see “Damage initiation for ductile metals,” Section 19.2.2 of the ABAQUS Analysis User's Manual).
The strain-based FLD criterion is limited to applications where the strain path is linear. On the other hand, the stress-based FLSD criterion is relatively insensitive to changes in the strain path. However, this apparent independence of the stress-based limit curve due to the strain path may simply reflect the small sensitivity of the yield stress to changes in the plastic deformation. The M-K criterion can capture the effects of nonlinear strain paths accurately; however, it is computationally expensive, especially if large numbers of imperfection orientations are introduced. It has been verified that the results obtained using the MSFLD criterion are similar to those obtained using the M-K criterion but with a much reduced computational expense (see “Progressive damage and failure of ductile metals,” Section 2.2.20 of the ABAQUS Verification Manual). Therefore, in this example we choose the MSFLD damage initiation criterion for necking instability.
For specifying the MSFLD damage initiation criterion, the forming limit curve of the material is required. In ABAQUS this criterion can be specified by converting the forming limit curve from the space of major versus minor strains to the space of equivalent plastic strain versus ratio of principal strain rates. ABAQUS also allows direct specification of the forming limit curve for the MSFLD criterion (see “Müschenborn-Sonne forming limit diagram (MSFLD) criterion” in “Damage initiation for ductile metals,” Section 19.2.2 of the ABAQUS Analysis User's Manual). We use the forming limit curve based on the experimental work of Hooputra (2005). This curve is assumed to be valid at both the quasi-static and the dynamic strain rates. The parameter OMEGA used in conjunction with the MSFLD criterion to provide filtering of numerical noise in the evaluation of the ratio of principal strain rates is set to 0.001 in both cases (see “Damage initiation for ductile metals,” Section 19.2.2 of the ABAQUS Analysis User's Manual); this value is recommended for crashworthiness simulations.
Damage due to initiation, growth, and coalescence of voids leads to ductile failure in metals; the formation of cracks within shear bands leads to shear failure. ABAQUS offers phenomenological damage initiation criteria for both of these mechanisms. The ductile criterion is specified by providing the equivalent plastic strain at the onset of ductile damage as a function of stress triaxiality and strain rate. Similarly, the shear criterion is specified by providing the equivalent plastic strain at the onset of shear damage as a function of shear stress ratio and strain rate (see “Damage initiation for ductile metals,” Section 19.2.2 of the ABAQUS Analysis User's Manual). The data required for both of these criteria may be difficult to obtain through direct experimentation since it would require experiments spanning a range of stress triaxiality and shear stress ratio that may be difficult to achieve. Hooputra et al. (2004) have given simplified analytical expressions for the ductile and the shear failure criteria that require only a limited number of experiments. In this example we adopt those expressions; however, we ignore the orthotropy of the ductile fracture to be consistent with the assumption of isotropic plasticity made earlier.
For the ductile damage initiation criterion the equivalent plastic strain is given by the following function of the stress triaxiality, 
(Hooputra et al, 2004):
and 
correspond to the equivalent plastic strain at ductile damage initiation for equibiaxial tensile and equibiaxial compressive deformation, respectively. For isotropic materials the stress triaxiality in equibiaxial tensile deformation state, 
, is 
, and in equibiaxial compressive deformation state, 
, is 
. The definition of in ABAQUS, as a ratio of the equivalent mean stress to the Mises equivalent stress, differs from that used by Hooputra et al. (2004) by a factor of 
. Consequently, the value of 
used in the above expression is three times the value used in Hooputra et al. (2004). The above expression has three parameters that must be obtained experimentally: , 
, and 
. These parameters depend on the material, strain rate, and possibly the temperature. For each strain rate of interest, three experiments are needed at different values of stress triaxiality to obtain the three material parameters. can be obtained directly from the Erichsen test (
). Three-point bending of sheet coupons (with width/thickness > 4) under plane strain tension (
) and fracture at the notch root of waisted tensile coupons in uniaxial tension (
) may provide two additional experiments to determine and . In the Erichsen and three-point bending experiments the local fracture strain can be derived by placing a grid on the specimen's surface; in the waisted tensile experiment the fracture strain can be obtained from the sheet thickness in the fracture plane (Hooputra et al., 2004). For the aluminum alloy used in this example the experimentally obtained ductile failure parameters at quasi-static and dynamic strain rates (250 s–1) are listed in Table 2.1.16–1.For the shear damage initiation criterion the equivalent plastic strain at the onset of damage is given by the following function of the shear stress ratio, 
(Hooputra et al, 2004):
with 
, and 
and 
correspond to the equivalent plastic strain at shear damage initiation for equibiaxial tensile and equibiaxial compressive deformation, respectively. The parameters 
and 
correspond to the values of at and 
, respectively. This expression has four parameters that must be determined experimentally: 
, 
, 
, and 
. These parameters depend on the material and strain rate. Hooputra et al. (2004) have used tensile specimens with a groove (rectangular cross-section and groove depth=half the sheet thickness) at 
to the loading direction (
), specially designed tensile specimens with a groove parallel to the loading direction (pure shear, 
), and Erichsen tests (
) in conjunction with the above expression to determine , , and 
. The value of the material parameter is taken as 0.3. For the aluminum alloy used in this example the experimentally obtained shear failure parameters at quasi-static and dynamic strain rates (250 s–1) are listed in Table 2.1.16–2.Using the aforementioned expressions and the material parameters listed in Table 2.1.16–1 and Table 2.1.16–2, tabular data for ductile and shear damage initiation criteria can be generated as a function of stress triaxiality and shear stress ratio, respectively. This tabular data is provided in the ABAQUS input files. The above expressions may give very high values of the equivalent plastic strain at damage initiation when the stress triaxiality or the shear stress ratio is very small. A cut-off value of the equivalent plastic strain can be provided in such cases.
Damage evolution occurs once the damage initiation criteria are satisfied. Plastic displacement-based linear damage evolution law is used for each of the three damage initiation criterion. The value of the plastic displacement at which the damage variable reaches 1 is taken as 0.1. The default maximum degradation rule is used, and the elements are removed from the mesh once the maximum degradation has occurred (see “Maximum degradation and choice of element removal” in “Damage evolution and element removal for ductile metals,” Section 19.2.3 of the ABAQUS Analysis User's Manual).
For the axial crushing simulation a velocity initial condition is specified at the reference node of the planar rigid impactor in the global 1-direction.
For the three-point bending simulation all the degrees of freedom at the reference node of the rigid supports are constrained. A velocity boundary condition in the global 2-direction is specified at the reference node of the rigid punch with all the remaining degrees of freedom constrained.
For the axial crushing simulation all the degrees of freedom at the reference node associated with the rigid support are constrained. Furthermore, all of the degrees of freedom except that associated with the global 1-direction are constrained at the reference node of the planar rigid impactor.
The velocity boundary condition at the rigid punch applies the load in the three-point bending simulation. In the case of the axial crushing simulation the initial velocity of the planar rigid impactor loads the component.
Rigid body constraints are specified in both cases to form element-based rigid bodies. These rigid bodies form the support and apply loads to the aluminum extrusion.
For the three-point bending simulation a contact pair interaction is defined between the rigid punch and the node-based surface of the aluminum extrusion component. A general contact interaction is defined between the rigid cylinders forming the support and the element-based surface of the aluminum extrusion component. In addition, self-contact is defined between the element-based surfaces of the extruded component. A friction coefficient of 0.05 is used for the contact between the rigid cylinders and the extruded component, and a value of 0.15 is used for the self-contact.
For the axial crushing simulation a contact pair interaction is defined between the extruded component and the rigid support as well as between the component and the rigid impactor. A general contact interaction is used for self-contact between the surfaces of the extruded component. A friction coefficient of 0.15 is used for all of the contact interactions in this case.
For both the three-point bending and axial crushing cases, a penalty-type mechanical constraint is used for all of the contact pair definitions.
Both the three-point bending and the axial crushing analyses consist of one explicit dynamic step. The total simulation times in the three-point bending and the axial crushing cases are 0.0501 s and 0.072 s, respectively. Both the analyses consider geometric nonlinearity and use automatic time incrementation using element-by-element stable time increment estimates.
For both cases the field output request includes the following quantities: displacement, stress, strain, element status, and damage initiation criteria variables. The history output request consists of displacement, velocity, acceleration, and reaction force at the reference point of the top rigid cylinder (for the three-point bending simulation) and at the reference point of the rigid impactor and the supporting base (for the axial crushing simulation). Energy output variables are requested for the entire model.
The overall deformed shape of the aluminum extrusion obtained from the three-point bending simulation is shown in Figure 2.1.16–2, and the experimentally observed deformed shape (Hooputra et al. 2004) is shown in Figure 2.1.16–3. The elements that have failed at the end of the simulation are shown in Figure 2.1.16–4, mapped into the undeformed configuration. Good qualitative agreement is seen between the simulation results and experimental observations. The load-displacement history of the punch obtained from the simulation is compared with three different experimental results in Figure 2.1.16–5. Again, a very good match is observed, indicating the reliability of the simulation results. In Figure 2.1.16–5 the simulation results are plotted after applying the Butterworth filter with a cut-off frequency of 1000 (see “Applying Butterworth filtering to an X–Y data object,” Section 29.4.25 of the ABAQUS/CAE User's Manual).
The overall deformed shape including the failure patterns obtained from the axial crushing simulation is shown in Figure 2.1.16–7. The deformed shape and the failure patterns are qualitatively similar to those observed experimentally (Figure 2.1.16–8). The overall force-displacement response from the simulation (filtered using the Butterworth filter with a cut-off frequency of 1500) is compared with the results from three different experiments (Hooputra, 2005) in Figure 2.1.16–9. Again, a good qualitative match is seen, and the numerical results are within the experimentally observed scatter.
In conclusion, the results from both the quasi-static three-point bending and the dynamic axial crushing simulations match the experimental data very well. It is also concluded that the use of progressive damage and failure is essential to capture the overall deformation and failure behavior of thin-wall aluminum extrusion.
Input file to create and analyze the model.
Input file to create and analyze the model.
Barlat, F., D. J. Lege, and J. C. Brem, “A Six-Component Yield Function for Anisotropic Materials,” International Journal of Plasticity, vol. 7, pp. 693–712, 1991.
Hooputra, H., H. Gese, H. Dell, and H. Werner, “A Comprehensive Failure Model for Crashworthiness Simulation of Aluminium Extrusions,” International Journal of Crashworthiness, vol. 9, pp. 449–463, 2004.
Hooputra, H., Private Communication, 2005.
Figure 2.1.16–2 Final deformed shape of the aluminum extrusion in the quasi-static three-point bending simulation.
Figure 2.1.16–3 Deformed shape of the aluminum extrusion in the quasi-static three-point bending experiment (Hooputra et al., 2004).
Figure 2.1.16–4 Completely failed elements at the end of the three-point bending simulation mapped into the undeformed configuration.
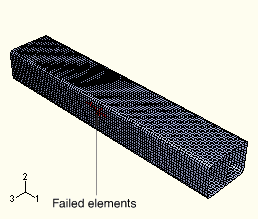
Figure 2.1.16–5 Comparison of the force-displacement response obtained from the three-point bending simulation with the experimental results of Hooputra et al. (2004).
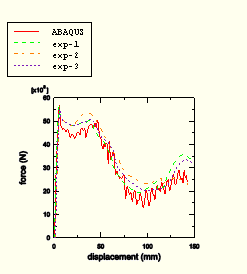
Figure 2.1.16–7 Final deformed shape of the aluminum extrusion in the dynamic axial crushing simulation.
)
