Products: ABAQUS/Standard ABAQUS/Design
Design sensitivity analysis in ABAQUS is performed using the semianalytical method. The issue of obtaining accurate sensitivities with respect to design shape parameters using this method has been discussed extensively in the literature (for example, Pedersen et al., 1989; Barthelemy and Haftka, 1990; Fenyes and Lust, 1991; and Van Keulen and De Boer, 1998). The difficulty is that the accuracy of the sensitivities can depend on the number of elements. This dependency is not seen with either analytical sensitivity analysis or with the overall finite difference method. A canonical example is a cantilever beam with an applied tip load, where the sensitivity of the tip displacement to the length of the beam is sought. This example demonstrates the effectiveness of the default perturbation sizing algorithm used by ABAQUS/Design in obtaining accurate tip displacement sensitivities. In addition, a sensitivity analysis is carried out to obtain the sensitivities of natural frequencies.
A cantilever beam 100 units long and 2 units deep is modeled using CPS8, S4R, and B31 elements. A resultant tip load of 1 unit is applied to the free end to simulate a shear load. The material is linear elastic, and a linear static analysis is carried out with ABAQUS/Standard. Four different mesh densities are used to study the effect of mesh refinement. The mesh densities chosen ensure that the error in the tip deflection compared to the Euler-Bernoulli solution is less than 0.05%. The coarsest mesh for each element type contains 50 elements along the length. The mesh density is doubled for each level of refinement, so the most refined mesh for each element type has 400 elements along the length. For the CPS8 element meshes, the coarsest mesh (50 elements along the length) contains one element through the depth and the most refined mesh (400 elements along the length) contains 8 elements through the depth. Only the axial coordinates of the nodes at the tip of the beam are assumed to depend on the length, so the gradients specified on the *PARAMETER SHAPE VARIATION option are unity (that is, only a boundary perturbation is applied).
Subsequent to the static analysis, a frequency analysis is performed including design sensitivity analysis. The sensitivities of the first three eigenvalues and corresponding natural frequencies with respect to the beam length are computed.
Based on Euler-Bernoulli beam theory the sensitivity of the tip displacement, 
, with respect to the length, 
, of the beam for a cantilever with end load 
is given by
is the modulus of elasticity and 
is the moment of inertia.The semianalytical method is based on perturbing the design parameter, , and using a differencing technique to approximate the sensitivities. For this problem the size of the perturbation in L yielding the most accurate tip displacement sensitivity 
can be determined by computing the error
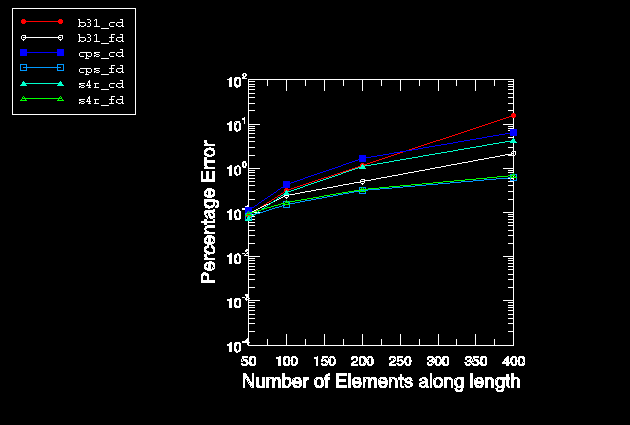
To demonstrate the growth in truncation error with the number of elements, perturbation sizes are chosen from the truncation region of the plot shown in Figure 1.17.1–1 such that the errors in the computed sensitivities for the most coarse meshes are acceptable (0.1%). This leads to perturbation sizes of 5 × 10–4, 1 × 10–3, and 1 × 10–3 for central differencing and 2 × 10–7, 6 × 10–7, and 9 × 10–7 for forward differencing for the CPS8, S4R, and B31 elements, respectively. These same perturbation sizes are then used in sensitivity analyses for the refined meshes. Figure 1.17.1–2 shows the growth in the percentage error in the computed sensitivities as the number of elements along the length is increased. It is clear from these results that the perturbation sizes yielding accurate results for a coarse mesh may yield poor results for a more refined mesh because the truncation error grows with mesh refinement. The truncation error can be controlled by proper choice of the perturbation size. Indeed, if one chooses a perturbation size of 1 × 10–9, it can be seen from Figure 1.17.1–3 that the growth in the error for both central differencing and forward differencing is insignificant for all element types.
The default perturbation sizing algorithm in ABAQUS/Design determines the perturbation sizes for each element, which are then used in a central difference scheme to compute the sensitivities. Table 1.17.1–1 shows the perturbation sizes chosen for the element that has the dominant influence on the tip displacement sensitivity at various levels of mesh refinement and the percentage error in the ABAQUS/Design sensitivity solution. For each of the coarsest meshes the perturbation size chosen by ABAQUS/Design is in good agreement with the optimum for central differencing based on Figure 1.17.1–1.
It can be shown that the sensitivities of the eigenvalues (
) and natural frequencies (f, in cycles/time) for a cantilever beam are given analytically by 
and 
, respectively. The frequency analysis is performed for the coarsest mesh, and the default perturbation sizing algorithm is used for the sensitivity analysis. By default, the algorithm determines the perturbation size based on the first mode, and the same perturbation size is then reused for the remaining modes. To force ABAQUS/Design to obtain a new perturbation size for each mode, the *DSA CONTROLS option can be used in the frequency step with the SIZING FREQUENCY parameter set to 1. The sensitivities of the eigenvalues and eigenfrequencies for the first three bending modes obtained with ABAQUS/Design are compared to those obtained analytically and using the overall central differencing method in Table 1.17.1–2, Table 1.17.1–3, and Table 1.17.1–4 for all element types. An optimum perturbation size of 1.0 × 10–4L was obtained by trial and error for the overall differencing method. An excellent agreement between ABAQUS and overall central differencing method is seen. The advantages of using the design sensitivity analysis capability in ABAQUS/Design over the overall finite difference method are: (1) automatic detemination of the perturbation size, and (2) reduced computational effort since the sensitivities are computed in the same analysis as the natural frequency extraction. The effort expended on recalculating the perturbation size for each mode by selecting a sizing frequency of 1 produces virtually no difference in the sensitivities, which are quite accurate with the default setting.
Cantilever beam modeled with 50 CPS8 elements, including frequency step.
Cantilever beam modeled with 100 CPS8 elements.
Cantilever beam modeled with 200 CPS8 elements.
Cantilever beam modeled with 400 CPS8 elements.
Cantilever beam modeled with 50 S4R elements, including frequency step.
Cantilever beam modeled with 100 S4R elements.
Cantilever beam modeled with 200 S4R elements.
Cantilever beam modeled with 400 S4R elements.
Cantilever beam modeled with 50 B31 elements, including frequency step.
Cantilever beam modeled with 100 B31 elements.
Cantilever beam modeled with 200 B31 elements.
Cantilever beam modeled with 400 B31 elements.
Pedersen, P., G. Cheng, and J. Rasmussen, “On Accuracy Problems for Semi-Analytical Sensitivity Analysis,” Mechanics of Structures and Machines, vol. 17, pp. 373–384, 1989.
Barthelemy, B., and R. T. Haftka, “Accuracy Analysis of the Semi-Analytic Method for Shape Sensitivity Calculation,” Mechanics of Structures and Machines, vol. 18, pp. 407–432, 1990.
Fenyes, P. A., and R. V. Lust, “Error Analysis of Semianalytic Displacement Derivatives for Shape and Sizing Variables,” AIAA Journal, vol. 29, pp. 271–279, 1991.
Van Keulen, F., and H. De Boer, “Rigorous Improvement of Semi-Analytical Design Sensitivities by Exact Differentiation of Rigid Body Motions,” International Journal for Numerical Methods in Engineering, vol. 42, pp. 71–91, 1998.
Table 1.17.1–1 ABAQUS tip displacement sensitivity results.
| Number of elements along the length | Perturbation size chosen by ABAQUS for the dominant element | Percentage error | ||||
|---|---|---|---|---|---|---|
| CPS8 | S4R | B31 | CPS8 | S4R | B31 | |
| 50 | 1.5e–06 | 1.5e–06 | 1.5e–08 | –0.004 | –0.002 | –0.002 |
| 100 | 1.5e–06 | 1.5e–07 | 1.5e–08 | 0.008 | –0.002 | –0.002 |
| 200 | 1.5e–06 | 1.5e–07 | 1.5e–08 | 0.009 | –0.002 | –0.002 |
| 400 | 1.5e–07 | 1.5e–07 | 1.5e–08 | 0.009 | –0.002 | –0.002 |
Table 1.17.1–2 Comparison of eigenvalue and frequency sensitivities obtained with ABAQUS and other methods for CPS8 element.
| Bending Mode | Mode Number | Sensitivity w.r.t. beam length | ABAQUS (default) | ABAQUS (SIZING FREQ=1) | Overall central differencing scheme | Analytic |
|---|---|---|---|---|---|---|
| 1 | 1 | Eigenvalue | –3.460e–03 | –3.460e–03 | –3.460e–03 | –3.461e–03 |
| Frequency | –9.362e–04 | –9.362e–04 | –9.350e–04 | –9.363e–04 | ||
| 2 | 2 | Eigenvalue | –1.355e–01 | –1.355e–01 | –1.353e–01 | –1.353e–01 |
| Frequency | –5.860e–03 | –5.860e–03 | –5.856e–03 | –5.859e–03 | ||
| 3 | 3 | Eigenvalue | –1.057e–00 | –1.057e–00 | –1.052e–00 | –1.058e–00 |
| Frequency | –1.630e–02 | –1.636e–02 | –1.630e–02 | –1.637e–02 |
Table 1.17.1–3 Comparison of eigenvalue and frequency sensitivities obtained with ABAQUS and other methods for S4R element.
| Bending Mode | Mode Number | Sensitivity w.r.t. beam length | ABAQUS (default) | ABAQUS (SIZING FREQ=1) | Overall central differencing scheme | Analytic |
|---|---|---|---|---|---|---|
| 1 | 4 | Eigenvalue | –3.460e–03 | –3.460e–03 | –3.460e–03 | –3.460e–03 |
| Frequency | –9.362e–04 | –9.362e–04 | –9.362e–04 | –9.362e–04 | ||
| 2 | 10 | Eigenvalue | –1.357e–01 | –1.357e–01 | –1.355e–01 | –1.353e–01 |
| Frequency | –5.860e–03 | –5.860e–03 | –5.856e–03 | –5.859e–03 | ||
| 3 | 17 | Eigenvalue | –1.062e–00 | –1.062e–00 | –1.060e–00 | –1.058e–00 |
| Frequency | –1.640e–02 | –1.640e–02 | –1.640e–02 | –1.637e–02 |
Table 1.17.1–4 Comparison of eigenvalue and frequency sensitivities obtained with ABAQUS and other methods for B31 element.
| Bending Mode | Mode Number | Sensitivity w.r.t. beam length | ABAQUS (default) | ABAQUS (SIZING FREQ=1) | Overall central differencing scheme | Analytic |
|---|---|---|---|---|---|---|
| 1 | 2 | Eigenvalue | –3.460e–03 | –3.460e–03 | –3.457e–03 | –3.461e–03 |
| Frequency | –9.366e–04 | –9.360e–04 | –9.370e–04 | –9.363e–04 | ||
| 2 | 4 | Eigenvalue | –1.353e–01 | –1.353e–01 | –1.354e–01 | –1.353e–01 |
| Frequency | –5.854e–03 | –5.854e–03 | –5.850e–03 | –5.859e–03 | ||
| 3 | 7 | Eigenvalue | –1.055e–00 | –1.055e–00 | –1.058e–00 | –1.058e–00 |
| Frequency | –1.634e–02 | –1.634e–02 | –1.639e–02 | –1.637e–02 |
Figure 1.17.1–1 Variation of error in tip displacement sensitivity with respect to the perturbation size.
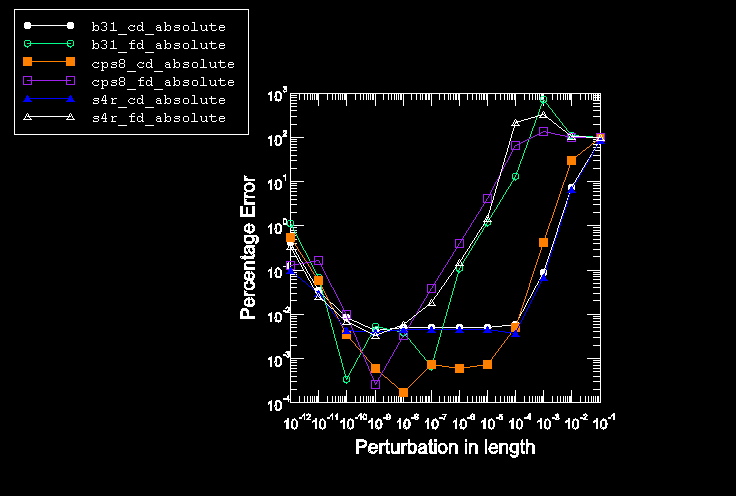
Figure 1.17.1–2 Variation of error in tip displacement sensitivity with mesh refinement for a perturbation size giving 0.1% error in 
for coarsest meshes (taken from Figure 1.17.1–1).
