Products: ABAQUS/Standard ABAQUS/Explicit
This example is intended to illustrate and verify the use of the tie constraint (*TIE) in a simple three-dimensional acoustic system, using several procedures.

This problem examines the natural frequencies of and the steady-state and transient wave propagation in a rectangular duct 20 meters in length and 1 meter square in cross-section. Figure 1.10.6–1 shows the three-dimensional test mesh. The model is split into two regions: one region has AC3D15 triangular prism elements (AC3D6 triangular prism elements in ABAQUS/Explicit), while the other has AC3D4 tetrahedral elements. Both regions are 10 meters long and are connected through tie constraints. Both regions are made of an acoustic material with a bulk modulus of 0.142 MPa and a density of 1.21 kg per cubic meter. The surface on the AC3D15 (AC3D6 in ABAQUS/Explicit) side is defined as the slave in the constraint pair.

The *FREQUENCY analysis uses no imposed boundary conditions or loads; in acoustic analysis this corresponds to rigid-wall (Neumann) boundary conditions on all exterior surfaces.
In the *STEADY STATE DYNAMICS problems the nodes on the right (unconstrained) end of the AC3D4 mesh are excited using the *BOUNDARY option on degree of freedom 8. A plane wave absorbing condition is imposed on the left end of the AC3D15 domain using the *IMPEDANCE option.
In the transient dynamic problems the same *BOUNDARY condition is applied but with a sinusoidal amplitude. The plane wave condition is imposed here, in the same manner as for the *STEADY STATE DYNAMICS problems.

The calculated frequencies obtained from the *FREQUENCY analysis correspond to analytic values, indicating that the constraint transmits the pressure between the mesh regions correctly.
The steady-state analyses are performed using the *STEADY STATE DYNAMICS, DIRECT option. The analyses are performed at selected frequencies from 5 to 100 Hz. Figure 1.10.6–2 shows the percentage error in the variable POR (pressure field magnitude) at 20 Hz. The mesh is viewed from the point of view opposite to that of Figure 1.10.6–1 to show the area of maximum error. The errors in the vicinity of the constraint are on the order of hundredths of a percent; the response in other regions of the mesh is more accurate.
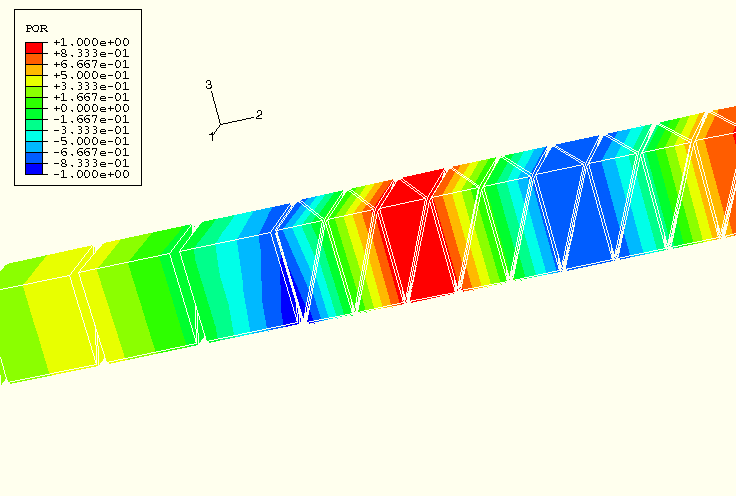
In the dynamic problem the ABAQUS/Standard analysis uses a fixed time increment of 0.0005 seconds. Figure 1.10.6–3 and Figure 1.10.6–4 show the variable POR (pressure magnitude) at a time of 0.04 seconds, shortly after the wavefront has crossed the *TIE boundary between the tetrahedra and the wedges. The *TIE constraints introduce minimal distortion and error in the solution.

Steady-state and natural frequency analysis.
Transient analysis.
Transient analysis.

Figure 1.10.6–2 Pressure magnitude error at 20 Hz, using *STEADY STATE DYNAMICS, DIRECT.
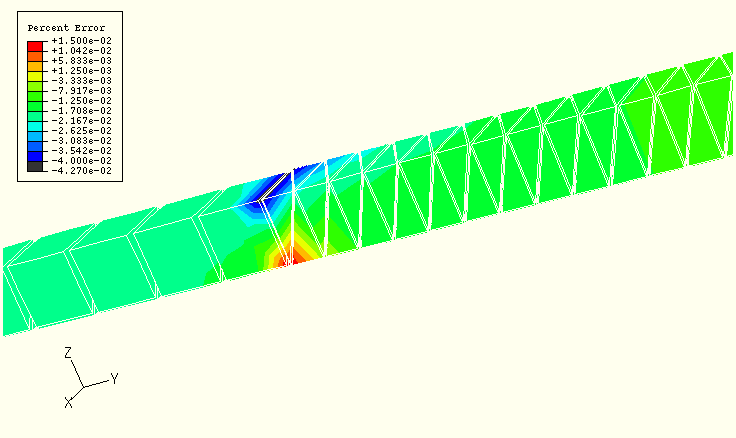
Figure 1.10.6–3 Pressure magnitude at 0.04 seconds, using *DYNAMIC.
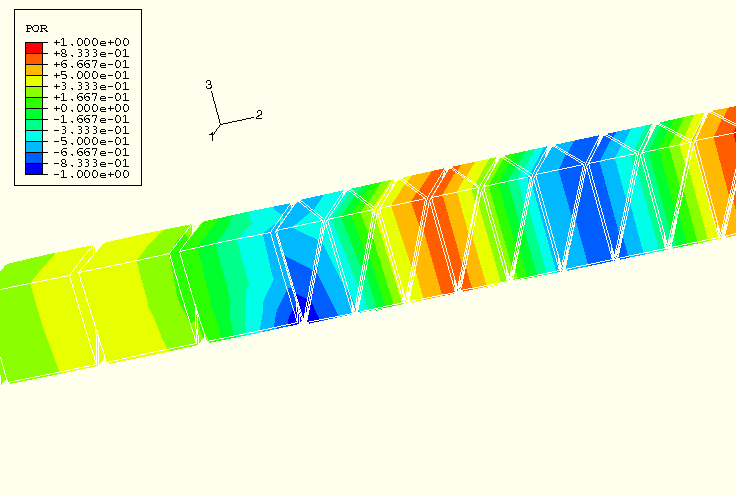
Figure 1.10.6–4 Pressure magnitude at 0.04 seconds, using *DYNAMIC, EXPLICIT.