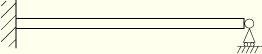Product: ABAQUS/Standard
The purpose of this example is to exercise the eigenvalue capability in ABAQUS with a variety of other options. This example uses two simple beam structures: a cantilever with various supports at the tip, and a beam with both ends simply supported. In some cases the beam is preloaded in an initial *STATIC step (“Static stress analysis,” Section 6.2.2 of the ABAQUS Analysis User's Manual), and the eigenvalues of the preloaded structure are then obtained (see also “Vibration of a cable under tension,” Section 1.4.3, where a prestressed cable vibration problem is studied). The preloaded structure analysis requires the large-displacement option by including the NLGEOM parameter on the *STEP option so that ABAQUS will form the initial stress matrix.
For the cantilever a variety of end conditions are used: a free end, a simple support, and a stiff, vertical spring support. In addition, cases are run with open and closed gap conditions at the end. In one case the beam is made up of separate segments, connected with the *EQUATION option (“Linear constraint equations,” Section 28.2.1 of the ABAQUS Analysis User's Manual).

The beam has a length of 127 mm (5 in), and a solid circular cross-section with a radius of 2.54 mm (0.1 in). Young's modulus is 187 GPa (27 × 106 lb/in2), and the density is 8015.19 kg/m3 (7.5 × 104 lb-s2/in4). The finite element model consists of 10 equal-sized cubic interpolation beam elements of type B23.

The following cases are analyzed:
Beam with both ends simply supported (see Figure 1.4.2–1):
Unstressed structure.
Structure prestressed by an axial force. The pretension force is 4448 N (1000 lb).
Cantilever beam (see Figure 1.4.2–2 to Figure 1.4.2–5):
Simple cantilever.
Pretensioned cantilever. The pretension force is 44482 N (10000 lb).
Gap condition at the free end—gap open. This case is the same as B1 above.
Gap condition at the free end—gap closed. This case is the same as B5 below.
Cantilever with a simple support at the end.
Cantilever with a spring support at the end. A stiff spring (stiffness 1.75127 × 103 MN/mm (107 lb/in)) is used, so that this case also corresponds to B5 above.
Cantilever beam with a simple support at the end. This case is the same as B5, but now the beam is defined geometrically as several separate segments, joined together kinematically by the *EQUATION option.

The results are given in Table 1.4.2–1 for the three lowest modes for all cases. In most cases they are compared to exact solutions, taken from Timoshenko (1937). As would be expected, with a 10 element mesh with cubic interpolation, the lowest three modes agree closely with the exact solutions. The pretensioned cases show the expected increase in frequencies over the same cases without pretensioning.

Basic simply supported case.
Pretensioned, simply supported case.
Basic cantilever case.
Pretensioned cantilever case.
Cantilever with a closed gap.
Cantilever with an open gap at the end.
Cantilever with a roller support.
Cantilever with a spring support at the free end.
Cantilever made up of two segments joined with the *EQUATION option.

Timoshenko, S., Vibration Problems in Engineering, D. Van Nostrand Company, Inc., New York, 2nd, 1937.

Table 1.4.2–1 Three lowest vibration frequencies of a beam.
| Case | Frequencies (Hz) | |||
|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | ||
| A1. | ABAQUS | 596.1 | 2384.6 | 5367.6 |
| Timoshenko | 596.1 | 2384.3 | 5364.7 | |
| A2. | ABAQUS | 882.7 | 2716.9 | 5711.9 |
| Timoshenko | 883.0 | 2717.1 | 5709.6 | |
| B1. | ABAQUS | 212.4 | 1330.8 | 3727.2 |
| Timoshenko | 212.3 | 1330.7 | 3726.4 | |
| B2. | ABAQUS | 1137.9 | 3624.4 | 6694.1 |
| B3. | ABAQUS | 212.4 | 1330.8 | 3727.2 |
| (same as case B1) | ||||
| B4. | ABAQUS | 931.2 | 3018.2 | 6300.7 |
| (same as case B5) | ||||
| B5. | ABAQUS | 931.2 | 3018.2 | 6300.7 |
| Timoshenko | 931.4 | 3018.0 | 6295.8 | |
| B6. | ABAQUS | 931.2 | 3017.9 | 6299.6 |
| (same as case B5) | ||||
| B7. | ABAQUS | 931.2 | 3018.2 | 6300.7 |
| (same as case B5) | ||||

Figure 1.4.2–1 Beam with simply supported ends. For Case A1 the preload is zero; for Case A2 the preload is 4448 N.
![]()
Figure 1.4.2–2 Cantilever beam. For Case B1 the preload is zero; for Case B2 the preload is 44482 N.

Figure 1.4.2–3 Cantilever beam with gap condition. For Case B3 the gap is open; for Case B4 the gap is closed.
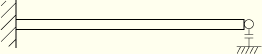
Figure 1.4.2–4 Cantilever beam with simply supported end. For Case B5 the beam is a single set of elements; for Case B7 the beam is defined as several separate segments joined with *EQUATION.