
Product: ABAQUS/Standard
![]()
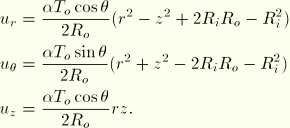
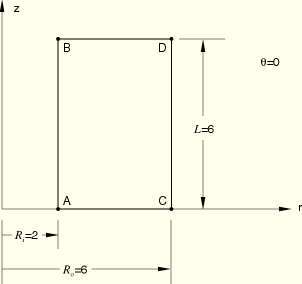
Only one-half of the structure is considered, with a symmetry plane at ![]() 0. The form of the displacement solution, which is a quadratic function in both
0. The form of the displacement solution, which is a quadratic function in both ![]() and
and ![]() , indicates that a single second-order element can model the structure adequately and yield accurate results. This problem is also solved with an 8 × 12 mesh of fully integrated first-order elements and a 16 × 24 mesh of reduced integration first-order elements.
, indicates that a single second-order element can model the structure adequately and yield accurate results. This problem is also solved with an 8 × 12 mesh of fully integrated first-order elements and a 16 × 24 mesh of reduced integration first-order elements.
Linear elastic, Young's modulus = 30 × 106, Poisson's ratio = 0.33, coefficient of thermal expansion = 1 × 10–4.
Boundary conditions:
![]() 0 on the
0 on the ![]() 0 plane;
0 plane; ![]() 0.06 is applied at
0.06 is applied at ![]() and
and ![]() 0 to eliminate the rigid body motion in the global
0 to eliminate the rigid body motion in the global ![]() -direction. This value of
-direction. This value of ![]() is obtained from the equation for
is obtained from the equation for ![]() above.
above.
Loading:
A temperature field of the form ![]() is applied. This is accomplished by calculating the temperature at each node and defining the temperature value using the *TEMPERATURE option.
is applied. This is accomplished by calculating the temperature at each node and defining the temperature value using the *TEMPERATURE option.
The analytical solution and the ABAQUS results for the CAXA8n, CAXA8Rn, CAXA4n, and CAXA4Rn (n = 1, 2, 3 or 4) elements are tabulated below for a structure with these parameters: ![]() 6,
6, ![]() 2,
2, ![]() 6, and
6, and ![]() 300. The output locations are at points
300. The output locations are at points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() on the
on the ![]() 0° plane, as shown in the figure on the previous page, and at points
0° plane, as shown in the figure on the previous page, and at points ![]() , and
, and ![]() , which are at the corresponding locations on the
, which are at the corresponding locations on the ![]() 180° plane. While both the CAXA8n and CAXA8Rn elements match the exact solution precisely with a zero state of stress, the models using the CAXA4n and CAXA4Rn elements fail to predict a stress-free state, even though the displacement solutions predicted are quite reasonable. However, the CAXA4Rn models give much more accurate results than the CAXA4n models. This example demonstrates that the fully integrated first-order elements do not handle bending problems very well.
180° plane. While both the CAXA8n and CAXA8Rn elements match the exact solution precisely with a zero state of stress, the models using the CAXA4n and CAXA4Rn elements fail to predict a stress-free state, even though the displacement solutions predicted are quite reasonable. However, the CAXA4Rn models give much more accurate results than the CAXA4n models. This example demonstrates that the fully integrated first-order elements do not handle bending problems very well.
| Variable | Exact | CAXA8 | CAXA8R | CAXA4 | CAXA4R |
|---|---|---|---|---|---|
| 0 | 0 | 0 | –14071 | 0.0168 | |
| 6 × 10–2 | 6 × 10–2 | 6 × 10–2 | 6 × 10–2 | 6 × 10–2 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 11664 | –3.2186 | |
| –3 × 10–2 | –3 × 10–2 | –3 × 10–2 | –2.9644 × 10–2 | –2.9999 × 10–2 | |
| 6 × 10–2 | 6 × 10–2 | 6 × 10–2 | 6.0312 × 10–2 | 6.0001 × 10–2 | |
| 0 | 0 | 0 | –14076 | 0.0162 | |
| 1.4 × 10–2 | 1.4 × 10–2 | 1.4 × 10–2 | 1.3993 × 10–2 | 1.4 × 10–2 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 11108 | –3.5190 | |
| 5 × 10–2 | 5 × 10–2 | 5 × 10–2 | 5.0306 × 10–2 | 5.0001 × 10–2 | |
| 18 × 10–2 | 18 × 10–2 | 18 × 10–2 | 17.95 × 10–2 | 18 × 10–2 | |
| 0 | 0 | 0 | –14071 | –0.0168 | |
| –6 × 10–2 | –6 × 10–2 | –6 × 10–2 | –6 × 10–2 | –6 × 10–2 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | –11664 | 3.2186 | |
| 3 × 10–2 | 3 × 10–2 | 3 × 10–2 | 2.9644 × 10–2 | 2.9999 × 10–2 | |
| –6 × 10–2 | –6 × 10–2 | –6 × 10–2 | –6.0312 × 10–2 | –6.0001 × 10–2 | |
| 0 | 0 | 0 | 14076 | 3.5100 | |
| –1.4 × 10–2 | –1.4 × 10–2 | –1.4 × 10–2 | –1.3993 × 10–2 | –1.4 × 10–2 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 11108 | 3.5100 | |
| –5 × 10–2 | –5 × 10–2 | –5 × 10–2 | –5.0306 × 10–2 | –5.0001 × 10–2 | |
| –18 × 10–2 | –18 × 10–2 | –18 × 10–2 | –17.95 × 10–2 | –18 × 10–2 |
Note:
The results are independent of ![]() , the number of Fourier modes.
, the number of Fourier modes.
Figure 1.3.34–1 through Figure 1.3.34–4 show plots of the undeformed and deformed meshes, the applied asymmetric temperature field, the contours of ![]() , and the contours of
, and the contours of ![]() , respectively, for the CAXA84 model.
, respectively, for the CAXA84 model.
CAXA41 elements.
CAXA42 elements.
CAXA43 elements.
CAXA44 elements.
CAXA4R1 elements.
CAXA4R2 elements.
CAXA4R3 elements.
CAXA4R4 elements.
CAXA81 elements.
CAXA82 elements.
CAXA83 elements.
CAXA84 elements.
CAXA8R1 elements.
CAXA8R2 elements.
CAXA8R3 elements.
CAXA8R4 elements.