
Products: ABAQUS/Explicit ABAQUS/CAE

The Johnson-Cook plasticity model:
is a particular type of Mises plasticity model with analytical forms of the hardening law and rate dependence;
is suitable for high-strain-rate deformation of many materials, including most metals;
is typically used in adiabatic transient dynamic simulations;
can be used in conjunction with the Johnson-Cook shear failure model;
can be used in conjunction with the tensile failure model to model tensile spall or a pressure cutoff;
can be used in conjunction with the progressive damage and failure models in ABAQUS/Explicit (“Progressive damage and failure,” Section 11.6) to specify different damage initiation criteria and damage evolution laws that allow for the progressive degradation of the material stiffness and the removal of elements from the mesh; and
must be used in conjunction with either the linear elastic material model (“Linear elastic behavior,” Section 10.2.1) or the equation of state material model (“Equation of state,” Section 10.9.1).

A Mises yield surface with associated flow is used in the Johnson-Cook plasticity model.

Johnson-Cook hardening is a particular type of isotropic hardening where the static yield stress, ![]() , is assumed to be of the form
, is assumed to be of the form
![]()
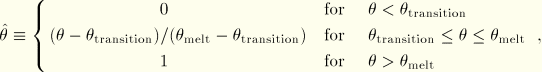
When ![]() , the material will be melted and will behave like a fluid; there will be no shear resistance since
, the material will be melted and will behave like a fluid; there will be no shear resistance since ![]() . The hardening memory will be removed by setting the equivalent plastic strain to zero. If backstresses are specified for the model, these will also be set to zero.
. The hardening memory will be removed by setting the equivalent plastic strain to zero. If backstresses are specified for the model, these will also be set to zero.
If you include annealing behavior in the material definition and the annealing temperature is defined to be less than the melting temperature specified for the metal plasticity model, the hardening memory will be removed at the annealing temperature and the melting temperature will be used strictly to define the hardening function. Otherwise, the hardening memory will be removed automatically at the melting temperature. If the temperature of the material point falls below the annealing temperature at a subsequent point in time, the material point can work harden again. For more details, see “Annealing or melting,” Section 11.2.5.
You provide the values of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as part of the metal plasticity material definition.
as part of the metal plasticity material definition.
| Input File Usage: | *PLASTIC, HARDENING=JOHNSON COOK |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |

Johnson-Cook strain rate dependence assumes that
![]()
![]()
![]()
is the yield stress at nonzero strain rate;
![]()
is the equivalent plastic strain rate;
![]() and
and ![]()
are material parameters measured at or below the transition temperature, ![]() ;
;
![]()
is the static yield stress; and
![]()
is the ratio of the yield stress at nonzero strain rate to the static yield stress (so that ![]() ).
).
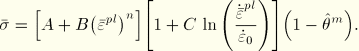
You provide the values of ![]() and
and ![]() when you define Johnson-Cook rate dependence.
when you define Johnson-Cook rate dependence.
The use of Johnson-Cook hardening does not necessarily require the use of Johnson-Cook strain rate dependence, but the use of Johnson-Cook strain rate dependence does require the use of Johnson-Cook hardening.
| Input File Usage: | Use both of the following options: |
*PLASTIC, HARDENING=JOHNSON COOK *RATE DEPENDENT, TYPE=JOHNSON COOK |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |

The Johnson-Cook shear failure model can be used in conjunction with the Johnson-Cook plasticity model to define shear failure of the material (see “Dynamic failure models,” Section 11.2.8). The Johnson-Cook shear failure model is based on the value of the equivalent plastic strain at element integration points; failure is assumed to occur when the damage parameter exceeds 1. The damage parameter, ![]() , is defined as
, is defined as
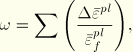
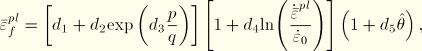
When this failure criterion is met, the deviatoric stress components are set to zero and remain zero for the rest of the analysis. Depending on your choice, the pressure stress may also be set to zero for the rest of calculation (if this is the case, you must specify element deletion and the element will be deleted) or it may be required to remain compressive for the rest of the calculation (if this is the case, you must choose not to use element deletion). By default, the elements that meet the failure criterion are deleted.
The Johnson-Cook shear failure model is suitable for high-strain-rate deformation of metals; therefore, it is most applicable to truly dynamic situations. For quasi-static problems that require element removal, the progressive damage and failure models (“Progressive damage and failure,” Section 11.6) or the Gurson metal plasticity model (“Porous metal plasticity,” Section 11.2.9) are recommended.
The use of the Johnson-Cook shear failure model requires the use of Johnson-Cook hardening but does not necessarily require the use of Johnson-Cook strain rate dependence. However, the rate-dependent term in the Johnson-Cook shear failure criterion will be included only if Johnson-Cook strain rate dependence is defined.
| Input File Usage: | Use both of the following options: |
*PLASTIC, HARDENING=JOHNSON COOK *SHEAR FAILURE, TYPE=JOHNSON COOK, ELEMENT DELETION=YES or NO |
| ABAQUS/CAE Usage: | Johnson-Cook shear failure is not supported in ABAQUS/CAE. |

The tensile failure model can be used in conjunction with the Johnson-Cook plasticity model to define tensile failure of the material. The tensile failure model uses the hydrostatic pressure stress as a failure measure to model dynamic spall or a pressure cutoff and offers a number of failure choices including element removal. Similar to the Johnson-Cook shear failure model, the ABAQUS/Explicit tensile failure model is suitable for high-strain-rate deformation of metals and is most applicable to truly dynamic problems. For more details, see “Dynamic failure models,” Section 11.2.8.
| Input File Usage: | Use both of the following options: |
*PLASTIC, HARDENING=JOHNSON COOK *TENSILE FAILURE |
| ABAQUS/CAE Usage: | The tensile failure model is not supported in ABAQUS/CAE. |

In ABAQUS/Explicit the Johnson-Cook plasticity model can be used in conjunction with the progressive damage and failure models. The capability allows for the specification of one or more damage initiation criteria, including ductile, shear, forming limit diagram (FLD), forming limit stress diagram (FLSD), and Marciniak-Kuczynski (M-K) criteria. After damage initiation, the material stiffness is degraded progressively according to the specified damage evolution response. The models offer two failure choices, including the removal of elements from the mesh as a result of tearing or ripping of the structure. For more details, see “Progressive damage and failure,” Section 11.6. The progressive damage models allow for a smooth degradation of the material stiffness, making them suitable for both quasi-static and dynamic situations. This is a great advantage over the dynamic failure models discussed above.
| Input File Usage: | Use the following options: |
*PLASTIC, HARDENING=JOHNSON COOK *DAMAGE INITIATION *DAMAGE EVOLUTION |
| ABAQUS/CAE Usage: | The progressive damage and failure models are not supported in ABAQUS/CAE. |

ABAQUS/Explicit allows for an adiabatic thermal-stress analysis (“Adiabatic analysis,” Section 6.5.5) or fully coupled temperature-displacement analysis (“Fully coupled thermal-stress analysis,” Section 6.5.4) to be performed in which heat generated by plastic straining of a material is calculated. This method is typically used in the simulation of bulk metal forming or high-speed manufacturing processes involving large amounts of inelastic strain, where the heating of the material caused by its deformation is an important effect because of temperature dependence of the material properties. Since the Johnson-Cook plasticity model is motivated by high-strain-rate transient dynamic applications, temperature change in this model is generally computed by assuming adiabatic conditions (no heat transfer between elements). Heat is generated in an element by plastic work, and the resulting temperature rise is computed using the specific heat of the material.
This effect is introduced by defining the fraction of the rate of inelastic dissipation that appears as a heat flux per volume.
| Input File Usage: | Use all of the following options in the same material data block: |
*PLASTIC, HARDENING=JOHNSON COOK *SPECIFIC HEAT *DENSITY *INELASTIC HEAT FRACTION |
| ABAQUS/CAE Usage: | Use all of the following options in the same material definition: |
Property module: material editor:
Mechanical |

There are cases when we need to study the behavior of a material that has already been subjected to some work hardening. For such cases initial equivalent plastic strain values can be provided to specify the yield stress corresponding to the work hardened state (see “Initial conditions,” Section 19.2.1). An initial backstress, ![]() , can also be specified. The backstress
, can also be specified. The backstress ![]() represents a constant kinematic shift of the yield surface, which can be useful for modeling the effects of residual stresses without considering them in the equilibrium solution.
represents a constant kinematic shift of the yield surface, which can be useful for modeling the effects of residual stresses without considering them in the equilibrium solution.
| Input File Usage: | *INITIAL CONDITIONS, TYPE=HARDENING |
| ABAQUS/CAE Usage: | Initial hardening conditions are not supported in ABAQUS/CAE. |

The Johnson-Cook plasticity model can be used with any elements in ABAQUS/Explicit that include mechanical behavior (elements that have displacement degrees of freedom).

In addition to the standard output identifiers available in ABAQUS/Explicit (“ABAQUS/Explicit output variable identifiers,” Section 4.2.2), the following variables have special meaning for the Johnson-Cook plasticity model:
PEEQ | Equivalent plastic strain, |
STATUS | Status of element. The status of an element is 1.0 if the element is active and 0.0 if the element is not. |