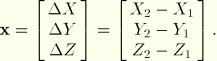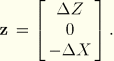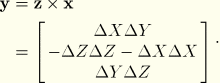Product: ABAQUS/CAE
Stress linearization is the separation of stresses through a section into constant membrane, linear bending, and nonlinearly varying peak stresses. The capability for calculating linearized stresses is available in the Visualization module of ABAQUS/CAE; it is most commonly used for two-dimensional axisymmetric models. See Chapter 33, “Calculating linearized stresses,” of the ABAQUS/CAE User's Manual for detailed information on how to obtain linearized stresses; the computational methods used by ABAQUS are discussed here.

Linearized stress components are computed using user-defined sections traversing a finite element model structure. Stress values are extracted at regular intervals along the defined section, and integration is performed numerically using the extracted stress values. Membrane, bending, and peak stress values are computed. These stresses are defined as follows:
Membrane stress
The constant portion of the normal stress such that a pure moment acts on a plane after the membrane stress is subtracted from the total stress.
Bending stress
The variable portion of the normal stress equal to the equivalent linear stress or, where no peak stresses exist, equal to the total stress minus the membrane stress.
Peak stress
The portion of the normal stress that exists after the membrane and bending stresses are subtracted from the total stress.
The membrane values of the stress components are computed using the following equation:

![]() is the membrane value of stress,
is the membrane value of stress,
![]() is the thickness of the section,
is the thickness of the section,
![]() is the stress along the path, and
is the stress along the path, and
![]() is the coordinate along the path.
is the coordinate along the path.
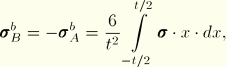
The integration is performed numerically. Assuming the path between point A and point B is divided uniformly into ![]() intervals, the integrals are evaluated as follows:
intervals, the integrals are evaluated as follows:
![]()
![]()
The derivation of the above equations is similar for the axisymmetric case, except for the fact that the neutral axis is shifted radially outward. Separate expressions are obtained for the stresses in the thickness, meridional, and hoop directions. In ABAQUS/CAE these are represented as local directions 1, 2, and 3, respectively (see Figure 2.17.1–2).
The meridional stresses are computed using the following relations. The meridional force per unit circumferential length is
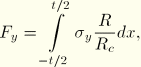
![]() is the stress in the meridional direction,
is the stress in the meridional direction,
![]() is the radius of the point being integrated, and
is the radius of the point being integrated, and
![]() is the mean circumferential radius.
is the mean circumferential radius.
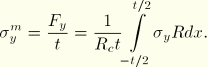
The numerical scheme used to compute the meridional membrane stress is
![]()
![]() is the meridional stress component at point
is the meridional stress component at point ![]() along the path and
along the path and
![]() is the radius at point
is the radius at point ![]() along the path.
along the path.
![]()
The meridional bending moment per unit circumferential length is defined as


Hence, the meridional bending stresses at the endpoints A and B are obtained with
![]()
![]()
The hoop membrane stress ![]() is obtained with
is obtained with
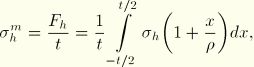
![]() is the hoop stress and
is the hoop stress and
![]() is the radius of curvature of the midsurface of the section in the meridional plane.
is the radius of curvature of the midsurface of the section in the meridional plane.
![]()
![]()

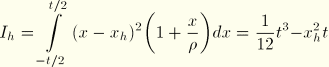
The numerical scheme to compute the circumferential membrane stress is
![]()
![]()
The thickness stress does not transfer any forces or moments. Typically, the stress arises due to applied external pressures and thermal expansion effects, and there is no obvious preferred method for determining “membrane” and “bending” stresses. Hence, we choose the thickness “membrane” stress as the average thickness stress:

![]()
The membrane shear stress in the meridional plane is computed in the same way as the meridional membrane stress:
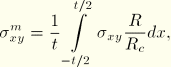
The shear stress distribution is assumed to be parabolic and equal to zero at the ends. Hence, the bending shear stresses are set to 0.0. The numerical scheme used to compute the membrane shear stress is:
![]()

The equations used when performing stress linearization in axisymmetric structures include the in-plane and out-of-plane radius of curvature of the stress line section. ABAQUS/CAE allows the inclusion of these “curvature correction” terms in the equations for nonaxisymmetric structures when computing the S22, S33, and S12 components. The numerical scheme is identical to that used when performing stress linearization in axisymmetric structures. The user is required to select a coordinate system in which to specify the curvature correction terms. An error will be generated when the ![]() -axis of the coordinate system is normal to the stress line.
-axis of the coordinate system is normal to the stress line.

Stress linearization requires the results to be transformed from the global coordinate system to a local coordinate system defined by the stress line.
The computation of the local coordinate system is a trivial procedure when performed for axisymmetric stress linearization. The transformation matrix in this case will be

When performing three-dimensional stress linearization, the local ![]() -axis will be defined by the stress line. The local
-axis will be defined by the stress line. The local ![]() - and
- and ![]() -axes are computed by a series of cross-products. This procedure is shown below.
-axes are computed by a series of cross-products. This procedure is shown below.
The vector between points (![]() ,
, ![]() ,
, ![]() ) and (
) and (![]() ,
, ![]() ,
, ![]() ) is
) is