Product: ABAQUS/Standard
The formulation described in this section provides a capability for modeling heat transfer with cavity thermal radiation (in addition to the radiation boundary conditions described in “Uncoupled heat transfer analysis,” Section 2.11.1). Cavities are defined in ABAQUS/Standard as collections of surfaces that are composed of facets. In axisymmetric and two-dimensional cases a facet is a side of an element; in three-dimensional cases a facet can be a face of a solid element or a surface of a shell element. For the purposes of the cavity radiation calculations, each facet is assumed to be isothermal and to have a uniform emissivity.
Based on the cavity definition, cavity radiation elements are created internally by ABAQUS. These elements can generate large matrices since they couple the temperature degree of freedom of every node on the cavity surface. Their Jacobian matrix is nonsymmetric: the nonsymmetric solution capability is automatically invoked if cavity radiation calculations are requested in the analysis. Both steady-state and transient capabilities are provided.
The theory on which this cavity radiation formulation is based is well-known and can be found in Holman (1990) and Siegel and Howell (1980). This section describes the formulation of the cavity radiation flux contributions and respective Jacobian for the Newton method used for the solution of the nonlinear radiation problem. The geometrical issues associated with the calculation of radiation viewfactors necessary in the formulation are addressed in “Viewfactor calculation,” Section 2.11.5.
Our formulation is based on gray body radiation theory that means that the monochromatic emissivity of the body is independent of the wavelength of propagation of the radiation. Only diffuse (nondirectional) reflection is considered. Attenuation of the radiation in the cavity medium is not considered. Using these assumptions together with the assumption of isothermal and isoemissive cavity facets, we can write the radiation flux per unit area into a cavity facet as
where
is the area of facet 
(seeing all cavity facets 
); 
are the emissivities of facets 
; 
is the Stefan-Boltzmann constant; 
is the geometrical viewfactor matrix; 
are the temperatures of facets ; 
is the absolute zero on the temperature scale used; and 
is the Kronecker delta.In the special case of blackbody radiation, where no reflection takes place (emissivity equal to one), Equation 2.11.4–1 reduces to
The variables used to solve the discrete approximation of the heat transfer problem with cavity radiation are the temperatures of the nodes on the cavity surface. Since we assume that for cavity radiation purposes each facet is isothermal, it is necessary to calculate an average facet temperature radiation power. To do so, we first define temperature radiation power as
refers to facet quantities and the superscript 
refers to nodal quantities.Then, we interpolate the average facet temperature radiation power from the facet nodal temperatures as
where is the number on nodes forming the facet and 
are nodal contribution factors calculated from area integration as 
are the interpolation functions for facet .The radiation flux into facet can now be written as
This can be rewritten as
where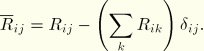
The nodal contributions from the radiation flux on each facet can now be written as
is 
Substituting Equation 2.11.4–3 and Equation 2.11.4–4 in the above equation:
where
The radiation flux 
is evaluated based on temperatures at the end of the increment, coordinates at the end of the increment, and emissivities at the beginning of the increment. Any time variation of the coordinates during the heat transfer analysis is predefined as translational and/or rotational motion and, therefore, provides no contribution to the Jacobian. Any variation of the emissivities as a function of temperature and predefined field variable changes with time is treated explicitly (values at the beginning of the increment are used) and, therefore, also provides no contribution to the Jacobian. The user can specify the maximum allowable emissivity change during an increment of the heat transfer analysis. Thus, the only Jacobian contribution is provided by temperature variations.
The Jacobian contribution arising from the cavity radiation flux is then written trivially as
In all practical cases the Jacobian is unsymmetric. This exact unsymmetric Jacobian is always used when cavity radiation analysis is performed.
