Products: ABAQUS/Standard
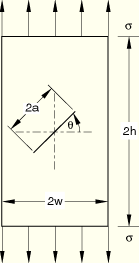
The model consists of a rectangular plate with a center slant crack subjected to far-field tension. The calculation is carried out using CPE8 elements with a linear elastic material. The geometrical ratios chosen for the plate are 
0.4 and 
2. The slant angle is 
45°. Displacement boundary conditions are prescribed on the top and bottom plate surfaces to apply tension to the plate so that consistent solutions can be obtained around the two crack tips. The total remote tensile load is obtained by summing the 
-direction nodal reaction forces on every node in the top or bottom plane; and the remote stress, 
, is defined as the total tensile force divided by the cross-sectional area of the plate.
The calculated stress intensity factors are compared with the solutions taken from Page 909 of the Stress Intensity Factors Handbook, edited by Y. Murakami.
Table 1.15.3–1 Nondimensional stress intensity factor results for isotropic elasticity. Contour 1 is omitted from the calculation.
 |  | |
|---|---|---|
| Reference solution | 0.5719 | 0.5290 |
| ABAQUS | 0.5540 | 0.5289 |
Based on the stress intensity factors 
and 
, ABAQUS can automatically predict the crack propagation direction, which is an angle 
measured with respect to the crack plane. For example, 
–52.41° if the maximum tangential stress criterion is used, –55.76° if the maximum energy release rate criterion is used, and –56.12° if the 
0 criterion is used.
ABAQUS also outputs the 
-integral value estimated by the stress intensity factors, 
= 3.4517 × 10–3, which agrees very well with the -integral value estimated directly, = 3.4515 × 10–3.
In addition, the stress intensity factors and the -integral are evaluated for the same plate using four different anisotropic, linear elastic materials: orthotropic elasticity specified by the engineering constants (denoted by ENGC), orthotropic elasticity specified by the stiffness parameters (ORTH), fully anisotropic elasticity (ANIS), and lamina elasticity (LAMI). The model with lamina elasticity is meshed using plane stress CPS8 elements. The results are summarized in Table 1.15.3–2. Though no published solutions are available for comparison, the -integrals from the stress intensity factors are in very good agreement with the -integrals evaluated directly.
Table 1.15.3–2 Nondimensional 
, 
, and values for a slant crack. Contour 1 is omitted from the average value calculation.
| Elasticity | -integral value estimated by the stress intensity factors | -integral value estimated directly | ||
|---|---|---|---|---|
 | |  × 103 |  × 103 | |
| ENGC | 0.5717 | 0.5299 | 2.8740 | 2.8750 |
| ORTH | 0.599 | 0.5429 | 2.1931 | 2.1930 |
| ANIS | 0.5388 | 0.5260 | 4.3790 | 4.3798 |
| LAMI | 0.5391 | 0.5223 | 4.7639 | 4.7637 |
Two-dimensional model for isotropic elasticity
Run the SlantCrackElasCPE8_model.py script to create the model. Then run the SlantCrackElasCPE8_job.py script to analyze the model.
Two-dimensional model for orthotropic elasticity specified by the engineering constants
Run the SlantCrackOrthEcCPE8_model.py script to create the model. Then run the SlantCrackOrthEcCPE8_job.py script to analyze the model.
Two-dimensional model for orthotropic elasticity specified by stiffness parameters
Run the SlantCrackOrthStCPE8_model.py script to create the model. Then run the SlantCrackOrthStCPE8_job.py script to analyze the model.
Two-dimensional model for anisotropic elasticity
Run the SlantCrackAnisoCPE8_model.py script to create the model. Then run the SlantCrackAnisoCPE8_job.py script to analyze the model.
Two-dimensional model for lamina elasticity
Run the SlantCrackLamCPS8_model.py script to create the model. Then run the SlantCrackLamCPS8_job.py script to analyze the model.
The following input files create models that have different meshes from the ABAQUS/CAE models created through the above Python scripts. The results are identical in both the cases.
Two-dimensional model for isotropic elasticity.
Node definitions.
Element definitions.
Two-dimensional model for orthotropic elasticity specified by the engineering constants.
Two-dimensional model for orthotropic elasticity specified by stiffness parameters.
Two-dimensional model for anisotropic elasticity.
Two-dimensional model for lamina elasticity.