Product: ABAQUS/Standard
The purpose of this example is to illustrate the use of the residual modes capability in ABAQUS and to verify the solution accuracy.
In many modal response analyses, simplifying a model by reducing the number of degrees of freedom or extracting only a small subset of eigenmodes is often a common practice. These assumptions are beneficial for cost reductions, but the accuracy of the modal solution may suffer. To improve solution accuracy, the method of residual modes (see “Natural frequency extraction,” Section 6.3.5 of the ABAQUS Analysis User's Manual) can be employed. This method extracts an additional set of modes based on loading conditions to help correct for errors introduced by mode truncation. Residual modes are orthogonal to retained eigenmodes and to each other and are computed by specifying the RESIDUAL MODES parameter on the *FREQUENCY option.
A simple multiple-degree-of-freedom spring-mass system is used to demonstrate the capability of using residual modes to obtain high solution accuracy. The model consists of 4 masses and 5 springs, as shown in Figure 1.4.14–1. The assembled mass and stiffness matrices are as follows:
is applied to node 3 in the 
-direction, where
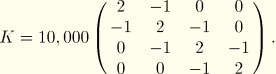
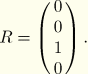
Only one eigenmode is extracted to demonstrate the capability of improving the solution accuracy by extracting residual modes. The residual mode (RM) obtained by ABAQUS is identical to that given in the reference.
| Mode No. | Frequency (Hz) | Nodal Eigendisplacements | |||
|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 3 | Node 4 | ||
| Published solutions | |||||
| 1 | 10.155 | 0.39948 | 0.63631 | 0.61408 | 0.03418 |
| RM | 21.865 | 0.68548 | 0.26428 | –0.58359 | –0.48927 |
| ABAQUS | |||||
| 1 | 10.155 | 0.39948 | 0.63631 | 0.61408 | 0.03418 |
| RM | 21.865 | 0.68548 | 0.26428 | –0.58359 | –0.48927 |
For the 3 Hz harmonic response analysis, displacements and accelerations of all the nodes are presented for two cases. The first case uses only the first eigenmode, while the second case uses both the first eigenmode and the residual mode. The percentage error shows very clearly how solution accuracy can be significantly improved by adding the residual modes to the original set of eigenvectors.
