Rayleigh damping options are provided in ABAQUS for both direct integration (*DYNAMIC) and modal superposition (*MODAL DYNAMIC) procedures. This example is intended to verify these Rayleigh damping options by comparing the ABAQUS results with an exact solution for a simple problem.

For direct integration Rayleigh damping is defined with the *DAMPING option in the material definition for those elements in which mass and stiffness proportional damping is desired. For modal dynamics analysis Rayleigh damping is defined in the MODAL DAMPING option in the step definition. For direct integration analysis Rayleigh damping can be introduced in any stress-based element, but it is not available for elements of type *SPRING; DASHPOT elements should be used in parallel with the SPRING elements for this purpose (see “Free and forced vibrations with damping,” Section 1.4.4). Elements with nonhomogeneous material damping properties are dealt with by taking a volume average of the damping coefficients. Stiffness proportional damping in nonlinear analysis is discussed in “Material damping,” Section 12.1.1 of the ABAQUS Analysis User's Manual.

The example is the simplest dynamic system: a massless truss connecting a point mass to ground. The mass is obtained by giving the material in the truss a density so that the lumped mass of the truss gives the correct point mass at the free end of the truss. The truss is initially stretched and then let go so that it undergoes vibrations of small amplitude. This is a linear problem; consequently, the response can be predicted using either the direct integration or modal dynamic procedures. These solutions are compared with each other and to the exact solution of the equation of motion.

Results and discussion

The equation of motion for the system is

where is the mass, the damping, the stiffness, and the displacement.

Rayleigh damping defines the damping as , where is the mass damping factor and is the stiffness damping factor.

Assuming a solution of the form , we have

where is the undamped frequency of vibration (25.118 rad/sec for the parameters of this example). Critical damping occurs when the value of causes the discriminant of this equation to be zero, so

We define the damping ratio, , as the ratio of damping to critical damping:

The relationships in this equation are often used as a basis for choosing and .

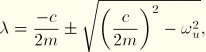
The equation defining can be rewritten

We choose the damping in this case to be less than critical, so 1 and the system can vibrate. The initial conditions are  1 and  0, so the dynamic part of the motion is

where is the damped frequency of the system.

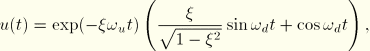
The amplitudes of this oscillatory equation before and after one period of vibration, , have the ratio

so the logarithmic decrement over cycles of response is

Table 1.4.5–1 shows the values of calculated from ABAQUS for the various test cases examined, together with their corresponding exact solution. A sample time history from which the logarithmic decrements are calculated is shown in Figure 1.4.5–2. All the ABAQUS runs use fixed time increments of .01 seconds. The integrator used in the modal method is exact, so the results of that analysis are exact. The integrator used in the direct integration method is not exact; however, since the period of the system is 0.25 seconds, the time increment chosen gives 25 increments per cycle, so those results are also quite accurate.

Table

Table 1.4.5–1 Exact versus graphical logarithmic decrements.

Damping parameters		Damping ratio,	Logarithmic decrement
Mass	Stiffness		Exact	Direct	Modal
				integration	superposition
1.00472	0.0	0.02	0.1257	0.1253	0.1257
0.0	1.59248 × 10–3	0.02	0.1257	0.1253	0.1257
1.00472	1.59248 × 10–3	0.04	0.2514	0.2499	0.2514