
Product: ABAQUS/Standard
The first papers on the vibration of thin, elastic, spherical shells precede the general formulation of the classical bending theory of shells. The problem of free vibration of a “complete” spherical shell was first examined by Lamb (1882). More detailed treatments were given by Baker (1961) and Silbiger (1962). The problem has many interesting features and serves well as a good test case for the shell elements in ABAQUS.
Thickness to radius ratios (![]() ) of 1/100 and 1/20 are considered. Although the shell is “thin” in either case, the thicker shell illustrates the significance of bending effects.
) of 1/100 and 1/20 are considered. Although the shell is “thin” in either case, the thicker shell illustrates the significance of bending effects.
All applicable shell elements in ABAQUS are used. For the axisymmetric case using SAX1 or SAX2 elements and the asymmetric-axisymmetric case using SAXA11, SAXA12, SAXA13, SAXA14, SAXA21, SAXA22, SAXA23, or SAXA24 elements, a well-refined mesh is used, with 80 nodes located at equal intervals along the circumference.
The meshes for the complete spherical shell using general shell elements use an identical number of elements for both the first-order and second-order formulations. Mesh convergence has not been studied. For the triangular shell elements each quadrilateral has been split into two triangles, without any consideration of preserving mesh symmetry. The mesh used with the second-order elements is shown in Figure 1.4.1–1.

Based on the membrane theory of shells, it is known that the natural frequency spectrum of a hollow, thin, elastic sphere consists of two infinite sets of modes and that one set of an infinite number of modes is spaced within a finite frequency interval. The mode shapes of the shell are expressed in terms of Legendre polynomials of degree ![]() . For each value of
. For each value of ![]() there are two distinct frequencies. The smaller of the two frequencies forms the “lower branch.” The second or “upper branch” modes are primarily extensional. The first 10 frequencies are given in Table 1.4.1–1.
there are two distinct frequencies. The smaller of the two frequencies forms the “lower branch.” The second or “upper branch” modes are primarily extensional. The first 10 frequencies are given in Table 1.4.1–1.
The ![]() 0 mode consists of purely radial vibration. Its frequency lies well above all of the frequencies associated with modes in the lower branch. It can be seen in the table that the frequencies of the upper branch increase without limit as
0 mode consists of purely radial vibration. Its frequency lies well above all of the frequencies associated with modes in the lower branch. It can be seen in the table that the frequencies of the upper branch increase without limit as ![]() increases but that those of the lower branch approach the limit:
increases but that those of the lower branch approach the limit:
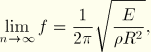
If only axisymmetric modes are considered, there is a distinct mode shape for each value of frequency. However, a model based on general shell elements allows for nonaxisymmetric modes. Interestingly, for the spherical shell the frequencies corresponding to nonaxisymmetric modes are identical to the frequencies of the axisymmetric modes. This is a consequence of the spherical symmetry of the shell. Corresponding to each value of ![]() there are
there are ![]() +1 linearly independent modes. To verify this, we have chosen to model the entire sphere, although the problem can be analyzed more economically by modeling a partial sphere using symmetry and antisymmetry boundary conditions. In addition, because of the multiple modes of identical frequency, this problem serves as a good test for the eigenvalue-eigenvector algorithms.
+1 linearly independent modes. To verify this, we have chosen to model the entire sphere, although the problem can be analyzed more economically by modeling a partial sphere using symmetry and antisymmetry boundary conditions. In addition, because of the multiple modes of identical frequency, this problem serves as a good test for the eigenvalue-eigenvector algorithms.
Table 1.4.1–2 summarizes the results obtained using the axisymmetric shell elements SAX1 and SAX2 for the first 10 modes. For the lower-order modes and the thinner shell case, the results agree well with membrane theory. The natural frequency of the ninth mode for ![]() 0.05 is significantly different from that predicted by membrane theory and is in agreement with Kalnins (1964). Membrane theory is clearly accurate for small values of
0.05 is significantly different from that predicted by membrane theory and is in agreement with Kalnins (1964). Membrane theory is clearly accurate for small values of ![]() and for the lower-order modes. The mode
and for the lower-order modes. The mode ![]() 1 corresponds to rigid body translation and is not shown in the table. In the axisymmetric case each frequency has a distinct mode shape and the eigenvalue iterations converge rapidly.
1 corresponds to rigid body translation and is not shown in the table. In the axisymmetric case each frequency has a distinct mode shape and the eigenvalue iterations converge rapidly.
Table 1.4.1–3 and Table 1.4.1–4 summarize the results obtained using the asymmetric-axisymmetric shell elements SAXA1N and SAXA2N (N=1, 2, 3 or 4). In this case for each value of ![]() there are
there are ![]() +1 modes instead of
+1 modes instead of ![]() +1, as predicted analytically. This is because, in the asymmetric-axisymmetric element formulation, symmetry with respect to the
+1, as predicted analytically. This is because, in the asymmetric-axisymmetric element formulation, symmetry with respect to the ![]() –
–![]() plane at
plane at ![]() 0 is assumed. However, for each
0 is assumed. However, for each ![]() the number of modes computed is limited by
the number of modes computed is limited by ![]() +1, where
+1, where ![]() is the number of Fourier interpolation terms used.
is the number of Fourier interpolation terms used.
Recall that, in the full models using general shell elements, there are ![]() +1 modes for each value of
+1 modes for each value of ![]() . To improve convergence in the eigenvalue iteration, we have, therefore, specified a higher number of trial vectors to be used. We calculate 18 eigenvalues to get the modes up to
. To improve convergence in the eigenvalue iteration, we have, therefore, specified a higher number of trial vectors to be used. We calculate 18 eigenvalues to get the modes up to ![]() 3. For higher-order modes such as
3. For higher-order modes such as ![]() 9, at least 100 or more eigenvalues need to be calculated. To keep this qualification test within a reasonable computational time, we have restricted the number of eigenvalues to 20. It implies that the bending effects will not be visible to the same extent as in the axisymmetric case. For this reason results from the general shell models are reported here only for the thin shell case with
9, at least 100 or more eigenvalues need to be calculated. To keep this qualification test within a reasonable computational time, we have restricted the number of eigenvalues to 20. It implies that the bending effects will not be visible to the same extent as in the axisymmetric case. For this reason results from the general shell models are reported here only for the thin shell case with ![]() 0.01.
0.01.
Table 1.4.1–5 provides the results for second-order shell elements; Table 1.4.1–6 provides the results for first-order shell elements. In these tables we list the first 20 eigenvalues, except the first six rigid body modes.
When second-order shell elements are used, the first five values (7 through 11) are almost identical to the membrane solution for the ![]() 2 case. The first-order mesh uses the same number of elements as the second-order mesh. Nevertheless, except for S3R elements, the results are quite accurate: the error is less than 2% for the first five eigenvalues. For S3R elements the maximum error is around 5% because these elements use a constant bending strain approximation. The accuracy can be increased by further refining the mesh. Eigenvalues 12 through 18 correspond to the mode
2 case. The first-order mesh uses the same number of elements as the second-order mesh. Nevertheless, except for S3R elements, the results are quite accurate: the error is less than 2% for the first five eigenvalues. For S3R elements the maximum error is around 5% because these elements use a constant bending strain approximation. The accuracy can be increased by further refining the mesh. Eigenvalues 12 through 18 correspond to the mode ![]() 3. It is observed that
3. It is observed that ![]() +1 modes are recovered, as predicted by the analytical solutions.
+1 modes are recovered, as predicted by the analytical solutions.
We also notice that the first-order triangular elements show more variance in eigenvalues corresponding to a given value of ![]() than the quadrilaterals. This is a consequence of orientation effects of the triangular element. The accuracy could be improved by designing the mesh to be spherically symmetric.
than the quadrilaterals. This is a consequence of orientation effects of the triangular element. The accuracy could be improved by designing the mesh to be spherically symmetric.
Figure 1.4.1–2 illustrates the modes ![]() 2 and
2 and ![]() 3 obtained with any of the shell models used.
3 obtained with any of the shell models used.
S3R element model.
S4 element model.
S4 element model (![]() 0.05).
0.05).
S4R element model.
S4R element model (![]() 0.05).
0.05).
S4R5 element model.
S8R element model.
S8R element model (![]() 0.05).
0.05).
S8R5 element model.
S9R5 element model.
STRI3 element model.
STRI65 element model.
SAX1 element model.
SAX1 element model (![]() 0.05).
0.05).
SAX2 element model.
SAX2 element model (![]() 0.05).
0.05).
SAXA11 element model (![]() 0.01).
0.01).
SAXA12 element model (![]() 0.01).
0.01).
SAXA13 element model (![]() 0.01).
0.01).
SAXA14 element model (![]() 0.01).
0.01).
SAXA21 element model (![]() 0.01).
0.01).
SAXA22 element model (![]() 0.01).
0.01).
SAXA23 element model (![]() 0.01).
0.01).
SAXA24 element model (![]() 0.01).
0.01).

Baker, W. E., “Axisymmetric Modes of Vibration of Thin Spherical Shells,” Journal of Acoustic Society of America, vol. 33, pp. 1749–1758, 1961.
Kalnins, A., “Effect of Bending on Vibration of Spherical Shells,” Journal of Acoustic Society of America, vol. 36, pp. 74–81, 1964.
Lamb, H., “On the Vibrations of a Spherical Shell,” Procedures of the London Mathematical Society, vol. 14, pp. 50–56, 1882.
Silbiger, A., “Nonaxisymmetric Modes of Vibration of Thin Spherical Shells,” Journal of Acoustic Society of America, vol. 34 862, 1962.

Table 1.4.1–1 Natural frequencies in cycles/sec based on membrane theory. (![]() 180.0 × 109,
180.0 × 109, ![]() 1/3,
1/3, ![]() 7670.0.)
7670.0.)
| Mode | Lower spectrum | Higher spectrum |
|---|---|---|
| 0 | – | 445.0 |
| 1 | 0.0 | 545.18 |
| 2 | 187.34 | 748.02 |
| 3 | 222.57 | 995.37 |
| 4 | 236.56 | 1256.58 |
| 5 | 239.56 | 1522.62 |
| 6 | 247.37 | 1791.24 |
| 7 | 249.80 | 2060.92 |
| 8 | 251.41 | 2331.42 |
| 9 | 252.54 | 2602.36 |
| 10 | 253.35 | 2873.62 |
Table 1.4.1–2 Natural frequencies with axisymmetric shell elements.
| Mode( | Membrane theory | ||||
|---|---|---|---|---|---|
| SAX1 | SAX2 | SAX1 | SAX2 | ||
| 2 | 187.34 | 187.26 | 187.36 | 187.72 | 187.82 |
| 3 | 222.57 | 222.30 | 222.69 | 225.19 | 225.57 |
| 4 | 236.56 | 236.15 | 236.95 | 245.35 | 246.09 |
| 5 | 239.56 | 243.12 | 244.41 | 264.61 | 265.76 |
| 6 | 247.37 | 247.43 | 249.30 | 289.13 | 290.66 |
| 7 | 249.80 | 250.76 | 253.29 | 321.84 | 323.68 |
| 8 | 251.41 | 253.99 | 257.25 | 364.00 | 366.02 |
| 9 | 252.54 | 257.66 | 261.69 | 415.81 | 417.88 |
| 10 | 253.35 | 262.18 | 267.00 | 445.14 | 445.14 |
Table 1.4.1–3 Natural frequencies with first-order asymmetric-axisymmetric shell elements.
| Eigenvalue number | SAXA11 | SAXA12 | SAXA13 | SAXA14 |
|---|---|---|---|---|
| 4 | 187.26 | 187.26 | 187.26 | 187.26 |
| 5 | 187.35 | 187.35 | 187.35 | 187.35 |
| 6 | 222.30 | 187.41 | 187.41 | 187.41 |
| 7 | 222.53 | 222.30 | 222.30 | 222.30 |
| 8 | 236.15 | 222.53 | 222.53 | 222.53 |
| 9 | 236.51 | 222.73 | 222.73 | 222.73 |
| 10 | 243.12 | 236.15 | 222.76 | 222.76 |
| 11 | 243.59 | 236.51 | 236.15 | 236.15 |
| 12 | 247.43 | 236.84 | 236.51 | 236.51 |
| 13 | 248.01 | 243.12 | 236.83 | 236.83 |
| 14 | 250.76 | 243.59 | 237.03 | 237.03 |
| 15 | 251.45 | 244.03 | 243.12 | 237.04 |
Table 1.4.1–4 Natural frequencies with second-order asymmetric-axisymmetric shell elements.
| Eigenvalue number | SAXA21 | SAXA22 | SAXA23 | SAXA24 |
|---|---|---|---|---|
| 4 | 187.36 | 187.36 | 187.36 | 187.36 |
| 5 | 187.36 | 187.36 | 187.36 | 187.36 |
| 6 | 222.69 | 187.36 | 187.36 | 187.36 |
| 7 | 222.69 | 222.69 | 222.69 | 222.69 |
| 8 | 236.94 | 222.69 | 222.69 | 222.69 |
| 9 | 236.95 | 222.69 | 222.69 | 222.69 |
| 10 | 244.41 | 236.94 | 222.69 | 222.69 |
| 11 | 244.41 | 236.95 | 236.95 | 236.95 |
| 12 | 249.29 | 236.95 | 236.95 | 236.95 |
| 13 | 249.30 | 244.41 | 236.95 | 236.95 |
| 14 | 253.29 | 244.41 | 236.95 | 236.95 |
| 15 | 253.30 | 244.41 | 244.41 | 236.95 |
Table 1.4.1–5 Natural frequencies with second-order general shell elements S8R, S8R5, S9R5, and STRI65.
| Eigenvalue number | S8R | S8R5 | S9R5 | STRI65 |
|---|---|---|---|---|
| 7 | 187.37 | 187.36 | 187.36 | 187.38 |
| 8 | 187.37 | 187.36 | 187.36 | 187.38 |
| 9 | 187.38 | 187.36 | 187.36 | 187.38 |
| 10 | 187.38 | 187.37 | 187.37 | 187.38 |
| 11 | 187.38 | 187.37 | 187.37 | 187.38 |
| 12 | 222.66 | 222.63 | 222.63 | 222.74 |
| 13 | 222.66 | 222.63 | 222.63 | 222.75 |
| 14 | 222.66 | 222.63 | 222.63 | 222.75 |
| 15 | 222.74 | 222.70 | 222.70 | 222.76 |
| 16 | 222.74 | 222.70 | 222.70 | 222.81 |
| 17 | 222.74 | 222.70 | 222.70 | 222.81 |
| 18 | 222.81 | 222.77 | 222.77 | 222.84 |
| 19 | 236.81 | 236.66 | 236.68 | 237.14 |
| 20 | 236.93 | 236.80 | 236.80 | 237.24 |
Table 1.4.1–6 Natural frequencies with first-order general shell elements S4R, S4R5, S4, STRI3, and S3R.
| Eigenvalue number | S4R | S4R5 | S4 | STRI3 | S3R |
|---|---|---|---|---|---|
| 7 | 189.97 | 189.97 | 189.86 | 187.32 | 190.19 |
| 8 | 189.97 | 189.97 | 189.86 | 188.76 | 190.66 |
| 9 | 190.05 | 190.05 | 190.04 | 188.76 | 190.66 |
| 10 | 190.05 | 190.05 | 190.06 | 189.97 | 192.25 |
| 11 | 190.05 | 190.05 | 190.06 | 189.97 | 192.25 |
| 12 | 223.71 | 223.70 | 225.66 | 223.85 | 229.55 |
| 13 | 223.71 | 223.70 | 225.74 | 224.16 | 230.82 |
| 14 | 223.71 | 223.70 | 225.74 | 224.16 | 230.82 |
| 15 | 227.90 | 227.89 | 228.59 | 227.51 | 233.47 |
| 16 | 227.90 | 227.89 | 228.59 | 228.71 | 234.32 |
| 17 | 227.90 | 227.89 | 228.61 | 228.71 | 234.82 |
| 18 | 231.43 | 231.37 | 233.57 | 229.06 | 234.82 |
| 19 | 233.48 | 233.45 | 237.24 | 239.45 | 252.14 |
| 20 | 233.59 | 233.45 | 242.00 | 239.50 | 252.14 |