Improving Explicit Congestion Notification with the Mark-Front Strategy 1

Chunlei Liu Raj Jain
Department of Computer and Information Science Chief Technology Officer, Nayna Networks, Inc.
The Ohio State University, Columbus, OH 43210-1277 157 Topaz St, Milpitas, CA 95035
cliu@cse.wustl.edu jain@acm.org

Abstract:

Delivering congestion signals is essential to the performance of networks. Current TCP/IP networks use packet losses to signal congestion. Packet losses not only reduces TCP performance, but also adds large delay. Explicit Congestion Notification (ECN) delivers a faster indication of congestion and has better performance. However, current ECN implementations mark the packet from the tail of the queue. In this paper, we propose the mark-front strategy to send an even faster congestion signal. We show that mark-front strategy reduces buffer size requirement, improves link efficiency and provides better fairness among users. Simulation results that verify our analysis are also presented. Keywords:Explicit Congestion Notification, mark-front, congestion control, buffer size requirement, fairness.

Introduction

Delivering congestion signals is essential to the performance of computer networks. In TCP/IP, congestion signals from the network are used by the source to determine the load. When a packet is acknowledged, the source increases its window size. When a congestion signal is received, its window size is reduced [ 1, 2]. TCP/IP uses two methods to deliver congestion signals. The first method is timeout. When the source sends a packet, it starts a retransmission timer. If it does not receive an acknowledgment within a certain time, it assumes congestion has happened in the network and the packet has been lost. Timeout is the slowest congestion signal because of the source has to wait a long time for the retransmission timer to expire. The second method is loss detection. In this method, the receiver sends a duplicate ACK immediately on reception of each out-of-sequence packet. The source interprets the reception of three duplicate acknowledgments as a congestion packet loss. Loss detection can avoid the long wait of timeout. Both timeout and loss detection use packet losses as congestion signals. Packet losses not only increase the traffic in the network, but also add large transfer delay. The Explicit Congestion Notification (ECN) proposed in [ 3, 4] provides a light-weight mechanism for routers to send a direct indication of congestion to the source. It makes use of two experimental bits in the IP header and two experimental bits in the TCP header. When the average queue length exceeds a threshold, the incoming packet is marked as congestion experiencedwith a probability calculated from the average queue length. When the marked packet is received, the receiver marks the acknowledgment using an ECN-Echobit in the TCP header to send congestion notification back to the source. Upon receiving the ECN-Echo, the source halves its congestion window to help alleviate the congestion. Many authors have pointed out that marking provides more information about the congestion state than packet dropping [ 5, 6], and ECN has been proven to be a better way to deliver congestion signal and exhibits a better performance [ 4, 5, 7]. In most ECN implementations, when congestion happens, the congested router marks the incoming packet that just entered the queue. When the buffer is full or when a packet needs to be dropped as in Random Early Detection (RED), some implementations, such as the nssimulator [ 8], have the ``drop from front'' option as suggested by Yin [ 9] and Lakshman [ 10]. A brief discussion of drop from front in RED can be found in [ 11]. However, for packet marking, these implementations still pick the incoming packet and not the front packet. We call this policy ``mark-tail''. In this paper, we propose a simple marking mechanism -- the ``mark-front'' strategy. This strategy marks a packet when the packet is going to leave the queue and the queue length is greater than the pre-determined threshold. The mark-front strategy is different from the current mark-tail policy in two ways. First, since the router marks the packet at the time when it is sent, and not at the time when the packet is received, a more up-to-date congestion signal is carried by the marked packet. Second, since the router marks the packet in the front of the queue and not the incoming packet, congestion signals do not undergo the queueing delay as the data packets. In this way, a faster congestion feedback is delivered to the source. The implementation of this strategy is extremely simple. One only needs to move the marking action from the enqueue procedure to the dequeue procedure and choose the packet leaving the queue in stead of the packet entering the queue. We justify the mark-front strategy by studying its benefits. We find that, by providing faster congestion signals, mark-front strategy reduces the buffer size requirement at the routers; it avoids packet losses and thus improves the link efficiency when the buffer size in routers is limited. Our simulations also show that mark-front strategy improves the fairness among old and new users, and alleviates TCP's discrimination against connections with large round trip time. The mark-front strategy differs from the ``drop from front'' option in that when packets are dropped, only implicit congestion feedback can be inferred from timeout or duplicate ACKs; when packets are marked, explicit and faster congestion feedback is delivered to the source. Gibbons and Kelly [ 6] suggested a number of mechanisms for packet marking, such as ``marking all the packets in the queue at the time of a packet loss'', ``marking every packet leaving the queue from the time of a packet loss until the queue becomes empty'', and ``marking packets randomly as they leave the queue with a probability so that later packets will not be lost.'' Our mark-front strategy differs from these marking mechanisms in that it is a simple marking rule that faithfully reflects the up-to-date congestion status, while the mechanisms suggested by Gibbons and Kelly either do not reflect the correct congestion status, or need sophisticated probability calculation about which no sound algorithm is known. It is worth mentioning that mark-front strategy is as effective in high speed networks as in low speed networks. Lakshman and Madhow [ 12] showed that the amount of drop-tail switches should be at least two to three times the bandwidth-delay product of the network in order for TCP to achieve decent performance and to avoid losses in the slow start phase. Our analysis in section 4.3 reveals that in the steady-state congestion avoidance phase, the queue size fluctuates from empty to one bandwidth-delay product. So the queueing delay experienced by packets when congestion happens is comparable to the fixed round-trip time. 2Therefore, the mark-front strategy can save as much as a fixed round-trip time in congestion signal delay, independent of the link speed. We should also mention that the mark-front strategy applies to both wired and wireless networks. When the router threshold is properly set, the coherence between consecutive packets can be used to distinguish packet losses due to wireless transmission error from packet losses due to congestion. This result will be reported elsewhere. This paper is organized as follows. In section 2 we describe the assumptions for our analysis. Dynamics of queue growth with TCP window control is studied in section 3. In section 4, we compare the buffer size requirements of mark-front and mark-tail strategies. In section 5, we explain why mark-front is fairer than mark-tail. The simulation results that verify our conclusions are presented in section 6. In section 7, we remove the assumptions made to facilitate the analysis, and apply the mark-front strategy to the RED algorithm. Simulation results show that mark-front has the advantages over mark-tail as revealed by the analysis.

Assumptions

ECN is used together with TCP congestion control mechanisms like slow start and congestion avoidance [ 2]. When the acknowledgment is not marked, the source follows existing TCP algorithms to send data and increase the congestion window. Upon the receipt of an ECN-Echo, the source halves its congestion window and reduces the slow start threshold. In the case of a packet loss, the source follows the TCP algorithm to reduce the window and retransmit the lost packet. ECN delivers congestion signals by setting the congestion experiencedbit, but determining when to set the bit depends on the congestion detection policy. In [ 3], ECN is proposed to be used with average queue length and RED. Their goal is to avoid sending congestion signals caused by transient traffic and to desynchronize sender windows [ 13, 14]. In this paper, to allow analytical modeling, we assume a simplified congestion detection criterion: when the actual queue lengthis smaller than the threshold, the incoming packet will not be marked; when the actual queue lengthexceeds the threshold, the incoming packet will be marked. We also make the following assumptions. (1) Receiver windows are large enough so the bottleneck is in the network. (2) Senders always have data to send and will send as many packets as their windows allow. (3) There is only one bottleneck link that causes queue buildup. (4) Receivers acknowledge every packet received and there are no delayed acknowledgments. (5) There is no ACK compression [ 15]. (6) The queue length is measured in packets and all packets have the same size.

Queue Dynamics with TCP Window Control

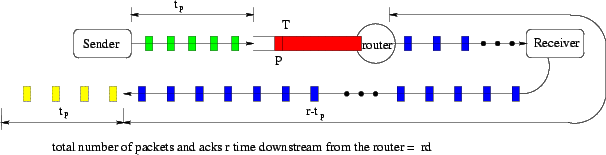
In this section, we study the relationship between the window size at the source and the queue size at the congested router. The purpose is to show the difference between mark-tail and mark-front strategies. Our analysis is made on one connection, but with small modifications, it can also apply to multiple connection case. Simulation results of multiple connections and connections with different round trip time will be presented in section 6. In a path with one connection, the only bottleneck is the first link with the lowest rate in the entire route. In case of congestion, queue builds up only at the router before the bottleneck link. The following lemma is obvious.

Lemma 1  If the data rate of the bottleneck link is dpackets per second, then the downstream packet inter-arrival time and the ack inter-arrival time on the reverse link can not be shorter than 1/dseconds. If the bottleneck link is fully-loaded (i.e., no idling), then the downstream packet inter-arrival time and the ack inter-arrival time on the reverse link are 1/dseconds.

Denote the source window size at time tas w(t), then we have

Theorem 1  Consider a path with only one connection and only one bottleneck link. Let the fixed round trip time be rseconds, the bottleneck link rate be dpackets per second, and the propagation and transmission time between the source and bottleneck router be tp. If the bottleneck link has been busy for at least rseconds, and a packet just arrived at the congested router at time t, then the queue length at the congested router is

 
Q(t)=w(t-tp)-rd. (1)


   
Figure 1: Calculation of the queue length
img1

ProofConsider the packet that just arrived at the congested router at time t. It was sent by the source at time t-tp. At that time, the number of packets on the path and outstanding acks on the reverse link was w(t-tp). By time t, tpdacks are received by the source. All packets between the source and the router have entered the congested router or have been sent downstream. As shown in Figure 1, the pipe length from the congested router to the receiver, and then back to the source is r-tp. The number of downstream packets and outstanding acks are (r-tp)d. The rest of the w(t-tp) unacknowledged packets are still in the congested router. So the queue length is

Q(t)=w(t-tp)-tpd- (r-tp)d= w(t-tp)-rd. (2)

This finishes the proof. Notice that in this theorem, we did not use the number of packets between the source and the congested router to estimate the queue length, because the packets downstream from the congested router and the acks on the reverse link are equally spaced, but the packets between the source and the congested router may not be. The analysis in this theorem is based on the assumptions in section 2. The conclusion applies to both slow start and congestion avoidance phases. In order for equation ( 1) to hold, the router must have been congested for at least rseconds.

Buffer Size Requirement and Threshold Setting

When ECN signals are used for congestion control, the network can achieve zero packet loss. When acknowledgments are not marked, the source gradually increase the window size. Upon the receipt of an ECN-Echo, the source halves its congestion window to reduce the congestion. In this section, we analyze the buffer size requirement for both mark-tail and mark-front strategies. The result also includes an analysis on how to set the threshold.

Mark-Tail Strategy

Suppose Pwas the packet that increased the queue length over the threshold T, and it was sent from the source at time s0and arrived at the congested router at time t0. Its acknowledgment, which was an ECN-echo, arrived at the source at time s1and the window was reduced at the same time. We also assume that the last packet before the window reduction was sent at time s1-and arrived at the congested router at time t1-. In order to use Theorem 1, we need to consider two cases separately: when Tis large and when Tis small, compared to rd.

Case 1

If Tis reasonably large (about rd) such that the buildup of a queue of size Tneeds rtime, the assumption in Theorem 1 is satisfied, we have

T=Q(t0)=w(t0-tp)-rd= w(s0)-rd, (3)

so

w(s0) = T+rd. (4)

Since the time elapse between s0and s1is one RTT, if packet Pwere not marked, the congestion window would increase to 2w(s0). Since Pwas marked, the congestion window before receiving the ECN-Echo was

w(s1-)=2w(s0)-1=2(T+rd)-1. (5)

When the last packet sent under this window reached the router at time t1-, the queue length was

 
Q(t1-)=w(s1-)-rd=2w(s0)-1 -rd= 2T+rd-1. (6)

Upon the receipt of ECN-Echo, the congestion window was halved. The source can not send any more packets before half of the packets are acknowledged. So 2T+rd-1 is the maximum queue length.

Case 2

If Tis small, rdis an overestimate of the number of downstream packets and acks on the reverse link.

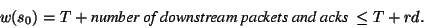img2 (7)

Therefore,

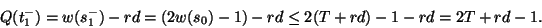img3 (8)

So, in both cases, 2T+rd-1 is an upper bound of queue length that can be reached in slow start phase.

Theorem 2  In a TCP connection with ECN congestion control, if the fixed round trip time is rseconds, the bottleneck link rate is dpackets per second, and the bottleneck router uses threshold Tfor congestion detection, then the maximum queue length can be reached in slow start phase is less than or equal to 2T+rd-1.

As shown by equation ( 6), when Tis large, the bound 2T+rd-1 can be reached with equality. When Tis small, 2T+rd-1 is just an upper bound. Since the queue length in congestion avoidance phase is smaller, this bound is actually the buffer size requirement.

Mark-Front Strategy

Suppose Pwas the packet that increased the queue length over the threshold T, and it was sent from the source at time s0and arrived at the congested router at time t0. The router marked the packet P' that stood in the front of the queue. The acknowledgment of P', which was an ECN-echo, arrived at the source at time s1and the window was reduced at the same time. We also suppose the last packet before the window reduction was sent at time s1-and arrived at the congested router at time t1-. Consider two cases separately: when Tis large and when Tis small.

Case 1

If Tis reasonably large (about rd) such that the buildup of a queue of size Tneeds rtime, the assumption in Theorem 1 is satisfied. We have

T=Q(t0)=w(t0-tp)-rd= w(s0)-rd, (9)

so

w(s0) = T+rd. (10)

In slow start phase, the source increases the congestion window by one for every acknowledgment it receives. If the acknowledgment of Pwas received at the source without the congestion indication, the congestion window would be doubled to

2w(s0)=2(T+rd).

However, when the acknowledgment of P' arrived, T-1 acknowledgments corresponding to packets prior to Pwere still on the way. So the window size at time s1-was

w(s1-)=2w(s0)-(T-1)-1=T+2rd. (11)

When the last packet sent under this window reached the router at time t1-, the queue length was

 
Q(t1-)=w(s1-)-rd=T+2rd-rd= T+rd. (12)

Upon the receipt of ECN-Echo, congestion window is halved. The source can not send any more packets before half of the packets are acknowledged. So T+rdis the maximum queue length.

Case 2

If Tis small, rdis an overestimate of the number of downstream packets and acks on the reverse link.

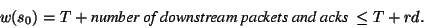img2 (13)

Therefore,

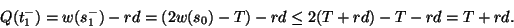img4 (14)

So, in both cases, T+rdis an upper bound of queue length that can be reached in the slow start phase.

Theorem 3  In a TCP connection with ECN congestion control, if the fixed round trip time is rseconds, the bottleneck link rate is dpackets per second, and the bottleneck router uses threshold Tfor congestion detection, then the maximum queue length that can be reached in slow start phase is less than or equal to T+rd.

Again, when Tis large, equation ( 12) shows the bound T+rdis tight. Since the queue length in congestion avoidance phase is smaller, this bound is actually the buffer size requirement. Theorem 2 and 3 estimate the buffer size requirement for zero-loss ECN congestion control.

Threshold Setting

In the congestion avoidance phase, congestion window increases roughly by one in every RTT. Assuming mark-tail strategy is used, using the same timing variables as in the previous subsections, we have

w(s0)=Q(t0)+rd=T+rd. (15)

The congestion window increases roughly by one in an RTT,

w(s1-)=T+rd+1. (16)

When the last packet sent before the window reduction arrived at the router, it saw a queue length of T+1:

Q(t1-)=w(s1-)-rd= T+1. (17)

Upon the receipt of the ECN-Echo, the window was halved:

w(s1)=(T+rd+1)/2. (18)

The source may not be able to send packets immediately after s1. After some packets were acknowledged, the halved window allowed new packets to be sent. The first packet sent under the new window saw a queue length of

Q(t1)=w(s1)-rd= (T+rd+1)/2-rd= (T-rd+1)/2. (19)

The congestion window was fixed for an RTT and then began to increase. So Q(t1) was the minimum queue length in a cycle. In summary, in the congestion avoidance phase, the maximum queue length is T+1 and the minimum queue length is (T-rd+1)/2. In order to avoid link idling, we should have 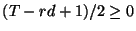img5or equivalently, 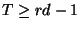img6. On the other hand, if minQis always positive, the router keeps an unnecessarily large queue and all packets suffer a long queueing delay. Therefore, the best choice of threshold should satisfy

(T-rd+1)/2 =0, (20)

or

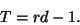img7 (21)

If mark-front strategy is used, the source's congestion window increases roughly by one in every RTT, but congestion feedback travels faster than the data packets. Hence

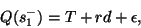img8 (22)

where 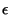img9is between 0 and 1, and depends on the location of the congested router. Therefore,

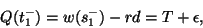img10 (23)


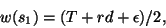img11 (24)


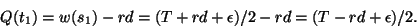img12 (25)

For the reason stated above, the best choice of threshold is 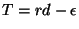img13. Compared with rd, the difference between 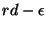img14and rd-1 can be ignored. So we have the following theorem:

Theorem 4  In a path with only one connection, the optimal threshold that achieves full link utilization while keeping queueing delay minimal in congestion avoidance phase is rd-1. If the threshold is smaller than this value, the link will be under-utilized. If the threshold is greater than this value, the link can be full utilized, but packets will suffer an unnecessarily large queueing delay.

Combining the results in Theorem 2, 3 and 4, we can see that the mark-front strategy reduces the buffer size requirement from about 3rdto 2rd. It also reduces the congestion feedback's delay by one fixed round-trip time.

Lock-out Phenomenon and Fairness

One of the weaknesses of mark-tail policy is its discrimination against new flows. Consider the time when a new flow joins the network, but the buffer of the congested router is occupied by packets of old flows. In the mark-tail strategy, the packet that just arrived will be marked, but the packets already in the buffer will be sent without being marked. The acknowledgments of the sent packets will increase the window size of the old flows. Therefore, the old flows which already have large share of the resources will grow even larger. However, the new flow with small or no share of the resources has to back off, since its window size will be reduced by the marked packets. This causes a ``lock-out'' phenomenon in which a single connection or a few flows monopolize the buffer space and prevent other connections from getting room in the queue [ 16]. Lock-out leads to gross unfairness among users and is clearly undesirable. Contrary to the mark-tail policy, the mark-front strategy marks the packets in the buffer first. Connections with large buffer occupancy will have more packets marked than connections with small buffer occupancy. Compared with the mark-tail strategy that let the packets in the buffer escape the marking, mark-front strategy helps to prevent the lock-out phenomenon. Therefore, we can expect that mark-front strategy to be fairer than mark-tail strategy. TCP's discrimination against connections with large RTT is also well known. The cause of this discrimination is similar to the discrimination against new connections. If connections with small RTT and large RTT start at the same time, the connections with small RTT will receive their acknowledgment faster and therefore grow faster. When congestion happens, connections with small RTT will take more buffer room than connections with large RTT. With mark-tail policy, packets already in the queue will not be marked but only newly arrived packets will be marked. Therefore, connections with small RTT will grow even larger, but connections with large RTT have to back off. Mark-front alleviates this discrimination by treating all packets in the buffer equally. Packets already in the buffer may also be marked. Therefore, connections with large RTT can have larger bandwidth.

Simulation Results


   
Figure 2: Simulation model.
img15

In order to compare the mark-front and mark-tail strategies, we performed a set of simulations with the nssimulator [ 8]. We modified the RED algorithm in nssimulator to deterministically mark the packets when the real queue length exceeds the threshold. The basic simulation model is shown in Figure 2. 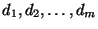A number of sources img16are connected to the router r1by 10 Mbps links, router r1is connected to r2by a 1.5 Mbps link, and destinations img17are connected to r2by 10 Mbps links. The link speeds are chosen so that congestion will only happen at the router r1, where mark-tail and mark-front strategies are tested. With the basic configuration shown in Figure 2, the fixed round trip time, including the propagation time and the transmission time at the routers, is 59 ms. Changing the propagation delay between router r1and r2from 20 ms to 40 ms gives an RTT of 99 ms. Changing the propagation delays between the sources and router r1gives us configurations of different RTT. An FTP application runs on each source. Reno TCP and ECN are used for congestion control. The data packet size, including all headers, is 1000 bytes and the acknowledgment packet size is 40 bytes. With the basic configuration,

img18

In our simulations, the routers perform mark-tail or mark-front. The results for both strategies are compared.

Simulation Scenarios

In order to show the difference between mark-front and mark-tail strategies, we designed the following simulation scenarios based on the basic simulation model described in Figure 2. If not specified, all connections have an RTT of 59 ms, start at 0 second and stop at the 10th second.
1.
One connection.
2.
Two connections with the same RTT.
3.
Two overlapping connections with the same RTT, but the first connection starts at 0 second and stops at the 9th second, the second connection starts at the first second and stops at the 10th second.
4.
Two connections with RTT equal to 59 and 157 ms respectively.
5.
Two connections with same RTT, but the buffer size at the congested router is limited to 25 packets.
6.
Five connections with the same RTT.
7.
Five connections with RRT of 59, 67, 137, 157 and 257 ms respectively.
8.
Five connections with the same RTT, but the buffer size at the congested router is limited to 25 packets.
Scenarios 1, 4, 6 and 7 are mainly designed for testing the buffer size requirement. Scenarios 1, 3, 4, 6, 7, 8 are for link efficiency, and scenarios 2, 3, 4, 5, 6, 7 are for fairness among users.

Metrics

We use three metrics to compare the two strategies. The first metric is the buffer size requirementfor zero loss congestion control. This is the maximum queue size that can be built up at the router in the slow start phase before the congestion signal takes effect at the congested router. If the buffer size is greater or equal to this value, no packet loss will happen. This metric is measured as the maximum queue length in the entire simulation. The second metric, link efficiency, is calculated from the number of acknowledged packets (not counting the retransmissions) divided by the possible number of packets that can be transmitted during the simulated time. Because of the slow start phase and possible link idling after the window reduction, the link efficiency is always smaller than 1. Link efficiency should be measured with long simulation time to minimize the effect of the initial transient state. We tried different simulation times from 5 seconds to 100 seconds. The results for 10 seconds show the essential features of the strategy, without much difference from the results for 100 seconds. So the simulation results presented in this paper are based on 10-second simulations. The third metric, fairnessindex, is calculated according to the formula in [ 17]. If m connections share the bandwidth, and xiis the number of acknowledged packets of connection i, then the fairnessindex is calculated as:

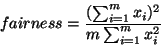img19 (26)

fairness index is often close to 1, in our graphs, we draw the unfairnessindex:

unfairness= 1- fairness. (27)

The performance of ECN depends on the selection of the threshold value. In our results, all three metrics are drawn for different values of threshold.

Buffer Size Requirement


   
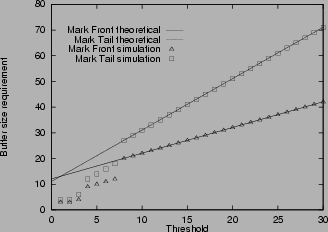
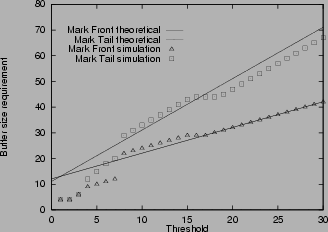
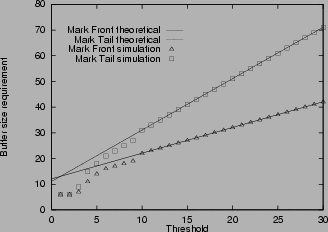
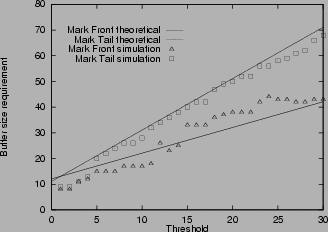
Figure 3: Buffer size requirement in various scenarios
img20 img21

One single connection

Two connections with different RTT

img22 img23

Five connections with same RTT

Five connections with different RTT


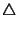Figure 3shows the buffer size requirement for mark-tail and mark-front. The measured maximum queue lengths are shown with `` img24'' and `` img25''. The corresponding theoretical estimates from Theorem 2 and 3 are shown with dashed and solid lines. In Figure 3(b) and 3(d), where the connections have different RTT, the theoretical estimate is calculated from the smallest RTT. From the simulation, we find that for connections with the same RTT, the theoretical estimate of buffer size requirement is accurate. When threshold Tis small, the buffer size requirement is an upper bound, when 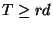img26, the upper bound is tight. For connections with different RTT, the estimate given by the largest RTT is an upper bound, but is usually an over estimate. The estimate given by the smallest RTT is a closer approximation.

Link Efficiency


   
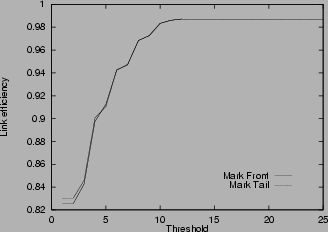
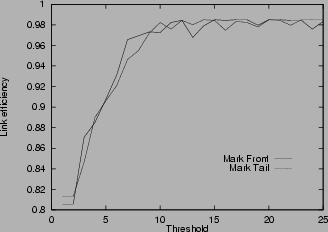
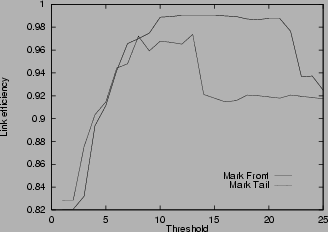
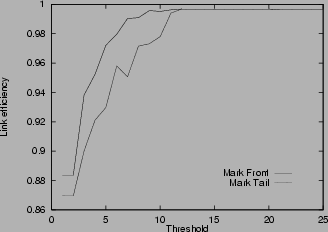
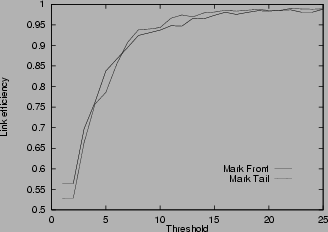
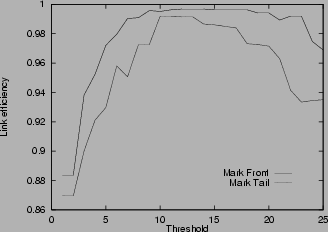
Figure 4: Link efficiency in various scenarios
img27 img28

One single connection

Two overlapping connections

img29 img30

Two same connections, limited buffer

Five connections with same RTT

img31 img32

Five connections with different RTT

Five same connections, limited buffer


Figure 4shows the link efficiency for various scenarios. In all cases, the efficiency increases with the threshold, until the threshold is about rd, where the link reaches almost full utilization. Small threshold results in low link utilization because it generates congestion signals even when the router is not really congested. Unnecessary window reduction actions taken by the source lead to link idling. The link efficiency results in Figure 4verify the choice of threshold stated in Theorem 4. In the unlimited buffer cases (a), (b), (d), (e), the difference between mark-tail and mark-front is small. However, when the buffer size is limited as in cases (c) and (f), mark-front has much better link efficiency. This is because when congestion happens, mark-front strategy provides a faster congestion feedback than mark-tail. Faster congestion feedback prevents the source from sending more packets that will be dropped at the congested router. Multiple drops cause source timeout and idling at the bottleneck link, and thus the low utilization. This explains the drop of link efficiency in Figure 4 (c) and (f) when the threshold exceeds about 10 packets for mark-tail and about 20 packets in mark-front.

Fairness


   
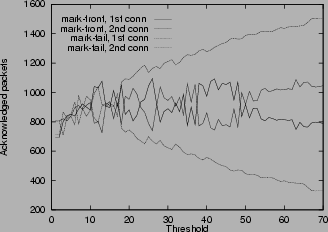
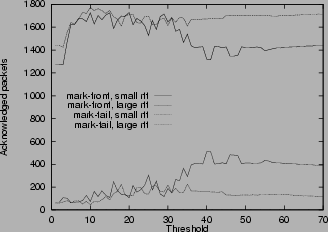
Figure 5: Lock-out phenomenon and alleviation by mark-front strategy
img33 img34

Two overlapping connections

Two connections with different RTT


Scenarios 2, 3, 4, 5, 6, 7 are designed to test the scenario of the two marking strategies. Figure 5shows lock-out phenomenon and alleviation by mark-front strategy. With the mark-tail strategy, old connections occupy the buffer and lock-out new connections. Although the two connections in scenario 3 have the same time span, the number of the acknowledged packets in the first connection is much larger than that of the second connection, Figure 5 (a). In scenario 4, the connection with large RTT (157 ms) starts at the same time as the connection with small RTT (59 ms), but the connection with small RTT grows faster, takes over a large portion of the buffer room and locks out the connection with large RTT. Of all of the bandwidth, only 6.49% is allocated to the connection with large RTT. Mark-front strategy alleviates the discrimination against large RTT by marking packets already in the buffer. Simulation results show that mark-front strategy improves the portion of bandwidth allocated to connection with large RTT from 6.49% to 21.35%.
   
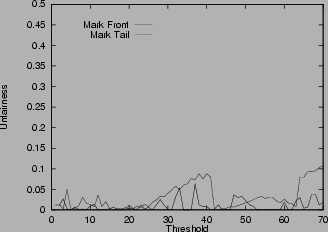
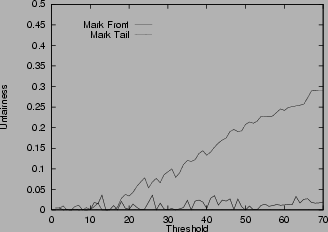
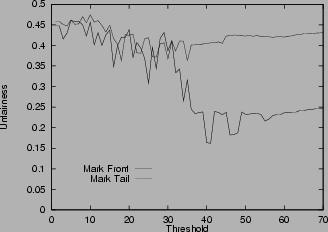
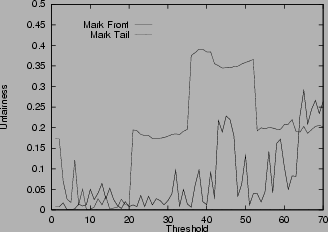
Figure 6: Unfairness in various scenarios
img35 img36

Two same connections

Two overlapping connections

img37 img38

Two connections with different RTT

Five same connections

img39 img40

Five same connections, limited buffer

Five connections with different RTT


Figure 6shows the unfairness index for the mark-tail and the mark-front strategies. In Figure 6 (a), the two connections have the same configuration. Which connection receives more packets than the other is not deterministic, so the unfairness index seems random. But in general, mark-front has smaller unfairness index than mark-tail. In Figure 6 (b), the two connections are different: the first connection starts first and takes the buffer room. Although the two connections have the same time span, if mark-tail strategy is used, the second connection is locked out by the first and therefore receives fewer packets. Mark-front avoids this lock-out phenomenon. The results show that the unfairness index of mark-front is much smaller than that of mark-tail. In addition, as the threshold increases, the unfairness index of mark-tail increases, but the mark-front remains roughly the same, regardless of the threshold. Figure 6 (c) shows the difference on connections with different RTT. With mark-tail strategy, the connections with small RTT grow faster and therefore locked out the connections with large RTT. Since mark-front strategy does not have the lock-out problem, the discrimination against connections with large RTT is alleviated. The difference of the two strategies is obvious when the threshold is large. Figure 6 (e) shows the unfairness index when the router buffer size is limited. In this scenario, when the buffer is full, the router drops the the packet in the front of the queue. Whenever a packet is sent, the router checks whether the current queue size is larger than the threshold. If yes, the packet is marked. The figure shows that mark-front is fairer than mark-tail. Similar results for five connections are shown in Figure 6 (d) and 6 (f).

Apply to RED

The analytical and simulation results obtained in previous sections are based on the simplified congestion detection model that a packet leaving a router is marked if the actual queue size of the router exceeds the threshold. However, RED uses a different congestion detection criterion. First, RED uses average queue size instead of the actual queue size. Second, a packet is not marked deterministically, but with a probability calculated from the average queue size. In this section, we apply the mark-front strategy to the RED algorithm and compare the results with the mark-tail strategy. Because of the difficulty in analyzing RED mathematically, the comparison is carried out by simulations only. RED algorithm needs four parameters: queue weight w, minimum threshold thmin, maximum threshold thmaxand maximum marking probability pmax. Although determining the best RED parameters is out of the scope of this paper, we have tested several hundred of combinations. In almost all these combinations, mark-front has better performance than mark-tail in terms of buffer size requirement, link efficiency and fairness. Instead of presenting individual parameter combinations for all scenarios, we focus on one scenario and present the results for a range of parameter values. The simulation scenario is the scenario 3 of two overlapping connections described in section 6.1. Based on the recommendations in [ 13], we vary the queue weight wfor four values: 0.002, 0.02, 0.2 and 1, vary thminfrom 1 to 70, fix thmaxas 2 thmin, and fix pmaxas 0.1. Figure 7shows the buffer size requirement for both strategies with different queue weight. In all cases, mark-front strategy requires smaller buffer size than the mark-tail. The results also show that queue weight wis a major factor affecting the buffer size requirement. Smaller queue weight requires larger buffer. When the actual queue size is used (corresponding to w=1), RED requires the minimum buffer size.
   
Figure 7: Buffer size requirement for different queue weight, pmax=0.1
img41 img42

w=0.002

w=0.02

img43 img44

w=0.2

w=1


Figure 8shows the link efficiency. For almost all values of threshold, mark-front provides better link efficiency than mark-tail. Contrary to the common belief, the actual queue size (Figure 8 (d)) is no worse than the average queue size (Figure 8 (a)) in achieving higher link efficiency.
   
Figure 8: Link efficiency for different queue weight, pmax=0.1
img45 img46

w=0.002

w=0.02

img47 img48

w=0.2

w=1


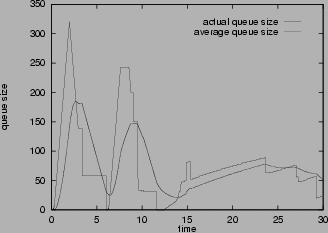
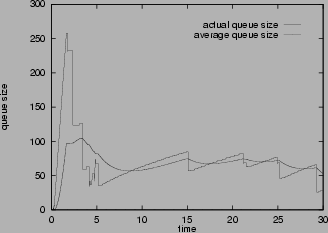
The queue size trace at the congested router shown in Figure 9provides some explanation for the smaller buffer size requirement and higher efficiency of mark-front strategy. When congestion happens, mark-front delivers faster congestion feedback than mark-tail so that the sources can stop sending packets earlier. In Figure 9 (a), with mark-tail signal, the queue size stops increasing at 1.98 second. With mark-front signal, the queue size stops increasing at 1.64 second. Therefore mark-front strategy needs smaller buffer. On the other hand, when congestion is gone, mark-tail is slow in reporting the change of congestion status. Packets leaving the router still carry the congestion information set at the time when they entered the queue. Even if the queue is empty, these packets still tell the sources that the router is congested. This out-dated congestion information is responsible for the link idling around 6th second and 12th second in Figure 9 (a). As a comparison, in Figure 9 (b), the same packets carry more up-to-date congestion information to tell the sources that the router is no longer congested, so the sources send more packets in time. Thus mark-front signal helps to avoid link idling and improve the efficiency.
   
Figure 9: Change of queue size at the congested router, w=0.002, thmin=70, thmax=140, pmax =0.1
img49 img50

Mark tail

Mark front


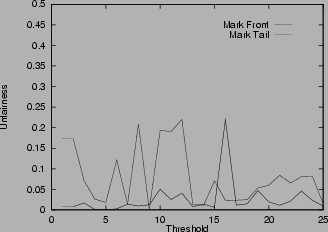
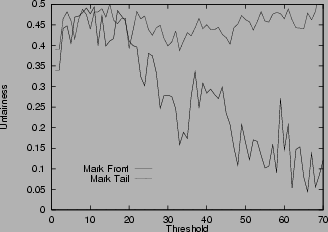
Figure 10shows the unfairness index. Both mark-front and mark-tail have big oscillations in the unfairness index when the threshold changes. These oscillations are caused by the randomness of how many packets of each connection get marked in the bursty TCP slow start phase. Changing the threshold value can significantly change the number of marked packets of each connection. In spite of the randomness, in most cases mark-front is fairer than mark-tail.
   
Figure 10: Unfairness for different queue weight, pmax=0.1
img51 img52

w=0.002

w=0.02

img53 img54

w=0.2

w=1


Conclusion

In this paper we analyze the mark-front strategy used in Explicit Congestion Notification (ECN). Instead of marking the packet from the tail of the queue, this strategy marks the packet in the front of the queue and thus delivers faster congestion signals to the source. Compared with the mark-tail policy, mark-front strategy has three advantages. First, it reduces the buffer size requirement at the routers. Second, it provides more up-to-date congestion information to help the source adjust its window in time to avoid packet losses and link idling, and thus improves the link efficiency. Third, it improves the fairness among old and new users, and helps to alleviate TCP's discrimination against connections with large round trip time. With a simplified model, we analyze the buffer size requirement for both mark-front and mark-tail strategies. Link efficiency, fairness and more complicated scenarios are tested with simulations. The results show that mark-front strategy achieves better performance than the current mark-tail policy. We also apply the mark-front strategy to the RED algorithm. Simulations show that mark-front strategy used with RED has similar advantages over mark-tail. Based on the analysis and the simulations, we conclude that mark-front is an easy-to-implement improvement that provides a better congestion control that helps TCP to achieve smaller buffer size requirement, higher link efficiency and better fairness among users.

Bibliography

1
V. Jacobson, Congestion avoidance and control, Proc. ACM SIGCOMM'88, pp. 314-329, 1988.

2
W. Stevens, TCP slow start, congestion avoidance, fast retransmit, and fast recovery algorithms, RFC 2001, January 1997.

3
K. Ramakrishnan and S. Floyd, A proposal to add Explicit Congestion Notification (ECN) to IP, RFC 2481, January 1999.

4
S. Floyd, TCP and explicit congestion notification, ACM Computer Communication Review, V. 24 N. 5, p. 10-23, October 1994.

5
J. H. Salim, U. Ahmed, Performance Evaluation of Explicit Congestion Notification (ECN) in IP Networks, Internet Draft draft-hadi-jhsua-ecnperf-01.txt, March 2000.

6
R. J. Gibbens and F. P. Kelly, Resource pricing and the evolution of congestion control, Automatica 35, 1999.

7
C. Chen, H. Krishnan, S. Leung, N. Tang, Implementing Explicit Congestion Notification (ECN) in TCP for IPv6, available at http://www.cs.ucla.edu/ ~ tang/papers/ECN_paper.ps, Dec. 1997.

8
UCB/LBNL/VINT Network Simulator - ns (version 2), http://www-mash.CS.Berkeley.EDU/ns/.

9
N. Yin and M. G. Hluchyj, Implication of dropping packets from the front of a queue, 7-th ITC, Copenhagen, Denmark, Oct 1990.

10
T. V. Lakshman, A. Neidhardt and T. J. Ott, The drop from front strategy in TCP and in TCP over ATM, Infocom96, 1996.

11
S. Floyd, RED with drop from front, email discussion on the end2end mailing list, ftp://ftp.ee.lbl.gov/email/sf.98mar11.txt, March 1998.

12
T. V. Laksman and U. Madhow. Performance Analysis of window-based flow control using TCP/IP: the effect of high bandwidth-delay products and random loss, in Proceedings of High Performance Networking, V. IFIP TC6/WG6.4 Fifth International Conference, Vol C, pp 135-149, June 1994.

13
S. Floyd and V. Jacobson, Random early detection gateways for congestion avoidance, IEEE/ACM Transactions on Networking, Vol. 1, No. 4, pp. 397-413, August 1993.

14
S. Blake, D. Black, M. Carlson, E. Davies, Z. Wang and W. Weiss, An architecture for differentiated services,, RFC 2475, December 1998.

15
L. Zhang, S. Shenker, and D. D. Clark, Observations and dynamics of a congestion control algorithm: the effects of two-way traffic, Proc. ACM SIGCOMM '91, pages 133-147, 1991.

16
B. Braden et al, Recommendations on Queue Management and Congestion Avoidance in the Internet, RFC 2309, April 1998.

17
R. Jain, The Art of Computer System Performance Analysis, John Wiley and Sons Inc., 1991.
Chunlei Liureceived his M.Sc degree in Computational Mathematics from Wuhan University, China in 1991. He received his M.Sc degrees in Applied Mathematics and Computer and Information Science from Ohio State University in 1997. He is now a PhD candidate in Department of Computer and Information Science at Ohio State University. His research interests include congestion control, quality of service, wireless networks and network telephony. He is a student member of IEEE and IEEE Communications Society.

Raj Jainis the cofounder and CTO of Nayna Networks, Inc - an optical systems company. Prior to this he was a Professor of Computer and Information Science at The Ohio State University in Columbus, Ohio. He is a Fellow of IEEE, a Fellow of ACM and a member of Internet Society, Optical Society of America, Society of Photo-Optical Instrumentation Engineers (SPIE), and Fiber Optic Association. He is on the Editorial Boards of Computer Networks: The International Journal of Computer and Telecommunications Networking, Computer Communications (UK), Journal of High Speed Networks (USA), and Mobile Networks and Applications. Raj Jain is on the Board of Directors of MED-I-PRO Systems, LLC, Pamona, CA, and MDeLink, Inc. of Columbus, OH. He is on the Board of Technical Advisors to Amber Networks, Santa Clara, CA. Previously, he was also on the Board of Advisors to Nexabit Networks Westboro, MA, which was recently acquired by Lucent Corporation. He is also a consultant to several networking companies. For further information and publications, please see http://www.cse.wustl.edu/~jain/.

Footnotes

... Strategy 1
This research was sponsored in part by grants from Nokia Corporation, Burlington, Massachusetts and NASA Glenn Research Center, Cleveland, Ohio.
... time. 2
The fixed round-trip time is the round-trip time under light load, i.e., without queueing delay.

Chunlei Liu
2000-09-14