| Chenliang Tian, <chenliang.t@wustl.edu> (A paper written under the guidance of Prof. Raj Jain) |
Download |
The integration of quantum and classical systems into hybrid quantum-classical networks (HQCNs) represents a pivotal advancement in the pursuit of quantum computing and secure communication. These networks leverage the unique capabilities of quantum mechanics, such as superposition and entanglement, while utilizing classical infrastructure for control and error management. However, the inherent fragility of quantum information due to decoherence and noise presents significant challenges that impede the practical realization of HQCNs.
This survey provides a comprehensive exploration of quantum error correction (QEC) methods crucial for maintaining the integrity of quantum information in HQCNs. We begin by introducing the foundational concepts of qubits, quantum gates, and quantum circuits, setting the stage for understanding the complexities of quantum errors. We delve into the types of quantum errors prevalent in quantum networks, including bit-flip, phase-flip, and more general noise models, illustrating their impact on quantum computations and communications.
The core of this survey examines existing QEC techniques, such as stabilizer codes, Calderbank-Shor-Steane codes, quantum low-density parity-check codes, fault-tolerant error correction, topological quantum codes, and concatenated codes. Through a storytelling approach, we elucidate how these methods address the unique challenges posed by quantum errors, highlighting their principles, strengths, and limitations.
Looking towards the future, we explore emerging directions that promise to enhance QEC in HQCNs. We discuss the application of reinforcement learning and other machine learning approaches for optimizing error correction, mechanisms to handle arbitrary multiple-qubit errors, software-based solutions, and the critical integration of QEC methods with quantum hardware. These advancements aim to overcome current limitations, paving the way for scalable and reliable quantum technologies.
By providing a thorough analysis of QEC in the context of hybrid networks, this survey underscores the importance of continued research and innovation. Our findings highlight the collaborative efforts required across disciplines to address the challenges of quantum error correction, ultimately contributing to the realization of robust quantum computing and communication systems.
Keywords: Quantum Error Correction, Hybrid Quantum-Classical Networks, Quantum Computing, Quantum Communication, Quantum Errors, Stabilizer Codes, Machine Learning in Quantum Computing, Fault-Tolerant Quantum Computation, Quantum Noise Mitigation, Quantum Networks, Reinforcement Learning, Topological Quantum Codes, Quantum Low-Density Parity-Check Codes, Quantum Hardware Integration, Quantum Information Science.
The advent of quantum computing heralds a new era in computational capabilities, promising to solve complex problems that are currently intractable for classical computers [Lapedus21][Gibney20]. These problems include factoring large numbers for cryptography, simulating quantum systems in chemistry and physics, and optimizing complex systems in logistics and machine learning [Yang23][Arute19]. Despite the tremendous potential, quantum computers face significant challenges, particularly in maintaining quantum coherence and managing errors due to decoherence and operational imperfections [Preskill18][Joshi21].
To bridge the gap between current quantum hardware limitations and the practical realization of quantum advantages, Hybrid Quantum-Classical Networks (HQCNs) have emerged as a promising approach [Bharti22][Endo21]. HQCNs integrate quantum and classical computational resources, leveraging the strengths of both paradigms. Quantum components perform tasks benefiting from quantum parallelism and entanglement, such as quantum simulations and optimization, while classical systems handle tasks like control logic, data preprocessing, and importantly, error correction [Mitarai18][Yang23]. This synergy enables more robust and scalable architectures capable of tackling real-world problems.
However, the realization of HQCNs is not without challenges. Quantum systems are inherently susceptible to errors from environmental interactions, leading to decoherence and loss of quantum information [Terhal15][Joshi21]. The fragility of quantum states necessitates the development of effective Quantum Error Correction (QEC) methods. Unlike classical error correction, QEC must contend with the no-cloning theorem and the need to correct both bit-flip and phase-flip errors simultaneously [Nielsen10][Gottesman10]. Moreover, implementing QEC in HQCNs requires careful coordination between quantum and classical components to manage error detection and correction without disrupting quantum operations [Roffe19].
This survey aims to explore the fundamental concepts of HQCNs, emphasizing the critical role of quantum error correction. We will examine their design principles, discuss the unique challenges posed by quantum errors, and review existing error correction methods. Furthermore, we will explore future directions in QEC research, including machine learning approaches and hardware integration strategies. Through this comprehensive analysis, we hope to provide insights into how HQCNs are shaping the future of computation and communication.
To embark on our exploration of quantum error correction within hybrid quantum-classical networks, let's first journey through the foundational landscape of quantum computing and networking. Imagine stepping into a world where the rules of classical physics give way to the counterintuitive phenomena of quantum mechanics-a realm where particles can exist in multiple states simultaneously, and entangled particles remain connected across vast distances. Understanding this world requires us to grasp several key concepts that form the building blocks of our discussion.
Picture a classical bit, the fundamental unit of information in traditional computing, holding a value of either 0 or 1. Now, envision a qubit, its quantum counterpart, which can exist in a superposition of both states at once. This means a qubit can be in state \(|0\rangle\), state \(|1\rangle\), or any quantum superposition of these states. Mathematically, we represent a qubit's state as:
Here, \(\alpha\) and \(\beta\) are complex numbers satisfying the normalization condition \(|\alpha|^2 + |\beta|^2 = 1\). This property allows qubits to encode and process a vast amount of information compared to classical bits [Nielsen10].
To visualize the state of a qubit, we often use the Bloch Sphere representation, where any pure qubit state is represented as a point on the surface of a sphere. This helps in understanding the geometric aspects of quantum states and their transformations. Figure 1 illustrates the Bloch Sphere with qubit states.
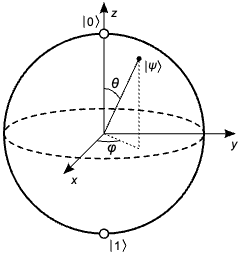
To manipulate qubits, we use quantum gates-operations that change their state through unitary transformations. Unlike classical logic gates, quantum gates like the Hadamard (H), Pauli-X, Pauli-Y, and Pauli-Z introduce superposition and entanglement, enabling quantum parallelism [Grover97]. For instance, applying a Hadamard gate to a qubit in state \(|0\rangle\) creates an equal superposition of \(|0\rangle\) and \(|1\rangle\).
Quantum circuits string together these gates to perform computations. Think of them as the quantum equivalent of classical circuits but operating under the principles of quantum mechanics. They can implement algorithms that solve specific problems exponentially faster than their classical counterparts, such as factoring large numbers with Shor's algorithm or searching unsorted databases with Grover's algorithm [Shor94][Grover97].
A particularly fascinating phenomenon is quantum entanglement. Imagine two qubits so deeply connected that the state of one instantaneously influences the state of the other, no matter how far apart they are. This "spooky action at a distance," as Einstein called it, is a cornerstone of quantum computing and quantum communication, enabling protocols like quantum teleportation and superdense coding [Ekert91].
However, measuring a qubit collapses its superposition, forcing it into one of its basis states. This measurement problem introduces challenges in quantum computing, as extracting information without disturbing the system is non-trivial [Nielsen10].
Now, let's extend our journey from individual quantum systems to networks of them. Quantum networks connect quantum devices across distances, allowing qubits to be transmitted and entangled states to be shared between nodes. These networks open doors to secure communication channels impervious to eavesdropping, thanks to the laws of quantum mechanics [Wehner18].
Imagine sending a secret message using quantum key distribution (QKD). Any attempt by an eavesdropper to intercept the qubits alters their state, alerting the communicating parties to the intrusion. This level of security is unattainable with classical encryption methods [Kimble08].
But transmitting qubits over long distances isn't straightforward. Quantum states are fragile and susceptible to decoherence-a process where interaction with the environment causes a loss of quantum information. To overcome this, quantum repeaters are introduced into the network. These devices extend the range of quantum communication by segmenting the transmission path and performing entanglement swapping and purification at each node, effectively "refreshing" the quantum states as they travel [Sangouard11].
A remarkable protocol enabled by entanglement is quantum teleportation. Contrary to science fiction depictions, quantum teleportation doesn't transport matter instantaneously but transfers the state of a qubit from one location to another without moving the qubit itself. This is achieved by utilizing an entangled pair and classical communication to transmit the necessary information to reconstruct the original state at the destination [Bouwmeester97].
In these networks, classical and quantum channels coexist harmoniously. Classical channels handle tasks like synchronizing operations and transmitting measurement results, while quantum channels carry the qubits and entangled states. This hybrid approach leverages the reliability of classical communication with the novel capabilities of quantum mechanics [Gyongyosi19].
As we delve deeper, we confront one of the most significant hurdles in quantum computing and communication: errors. In the classical world, error correction codes detect and correct errors by adding redundancy. For example, in a noisy communication channel, we might send multiple copies of a bit and use majority voting to determine the correct value. However, applying this strategy directly to quantum information isn't possible [Hamming50].
The first challenge arises from the no-cloning theorem, which states that it's impossible to create an identical copy of an arbitrary unknown quantum state. This prohibits the straightforward replication of qubits for redundancy purposes [Wootters82]. Consequently, we can't simply copy quantum data to protect it from errors.
Moreover, quantum errors are more complex than classical bit-flips. In addition to bit-flip errors (analogous to flipping a 0 to a 1), qubits can suffer from phase-flip errors, where the relative phase between quantum states is altered. Even more challenging are combinations of both, known as Y-errors. Quantum error correction codes must, therefore, detect and correct both types of errors simultaneously, a task that demands sophisticated coding schemes [Knill97].
Another obstacle is the measurement problem. Directly measuring a qubit to detect errors collapses its quantum state, destroying the very information we aim to protect. To circumvent this, quantum error correction employs indirect measurement techniques. By entangling the data qubits with ancillary qubits, we can measure the ancillas to extract error syndromes without disturbing the data qubits' superposition [Steane96].
These challenges highlight the necessity of developing new error correction methods tailored to quantum systems. Quantum error correction codes, such as the Shor code and the surface code, have been devised to protect quantum information, ensuring that the promise of quantum computing and communication can be realized despite the presence of noise and decoherence [Lidar13].
Understanding the intricacies of quantum error correction is crucial for advancing hybrid quantum-classical networks. By effectively managing errors, we can maintain coherence over longer periods and distances, paving the way for scalable quantum technologies that integrate seamlessly with classical infrastructure.
As we delve deeper into the quantum realm, we encounter the subtle yet formidable adversaries that threaten the integrity of quantum information: quantum errors. Unlike classical errors, which are typically straightforward bit flips, quantum errors are multifaceted due to the rich structure of quantum states. Understanding these errors is crucial for developing effective error correction strategies in quantum networks [Preskill18].
To summarize the primary types of quantum errors and their effects on qubits, Table 1 provides a concise overview.
| Error Type | Operator | Effect on Qubit |
|---|---|---|
| Bit-Flip Error | Pauli-X (\(X\)) | \(X|0\rangle = |1\rangle\), \(X|1\rangle = |0\rangle\) |
| Phase-Flip Error | Pauli-Z (\(Z\)) | \(Z|0\rangle = |0\rangle\), \(Z|1\rangle = -|1\rangle\) |
| Bit and Phase-Flip Error | Pauli-Y (\(Y\)) | \(Y|0\rangle = i|1\rangle\), \(Y|1\rangle = -i|0\rangle\) |
Understanding these error types allows us to develop targeted strategies for error correction. In the following subsections, we delve into each error type in detail.
The most intuitive type of quantum error is the bit-flip error, analogous to flipping a classical bit from 0 to 1 or vice versa. In the quantum world, a bit-flip error changes a qubit's state from \(|0\rangle\) to \(|1\rangle\) or from \(|1\rangle\) to \(|0\rangle\). This error is represented by the Pauli-X operator, often called the quantum NOT gate:
Mathematically, the Pauli-X operator is expressed as:
Bit-flip errors can occur due to interactions with the environment that cause energy exchanges, such as electromagnetic fluctuations. In quantum networks, they may happen during transmission over noisy channels or imperfect gate operations [Kandala19].
Moving beyond classical analogies, we encounter phase-flip errors. Unlike bit flips, phase flips alter the relative phase between the \(|0\rangle\) and \(|1\rangle\) states without changing the amplitudes. The Pauli-Z operator represents this error:
The Pauli-Z operator is given by:
Phase-flip errors arise from dephasing processes, where qubits lose coherence due to interactions with their environment that affect their phase. This type of error is uniquely quantum and has no direct classical counterpart [Kravets19].
The complexities deepen with Y-errors, which combine both bit-flip and phase-flip errors. Represented by the Pauli-Y operator, a Y-error applies both \(X\) and \(Z\) operations to a qubit:
In matrix form, the Pauli-Y operator is:
The action of \(Y\) on the computational basis states is:
Y-errors can result from more complex noise processes and represent the full spectrum of single-qubit errors. They highlight the need for quantum error correction codes capable of addressing all types of errors simultaneously [Vuillot19].
Beyond these fundamental errors, quantum systems are subject to various noise processes that can degrade quantum information. Understanding these noise models is essential for designing robust quantum networks.
Depolarizing Noise:Depolarizing noise is a model where a qubit randomly undergoes a Pauli error (\(X\), \(Y\), or \(Z\)) with certain probabilities, effectively losing all its quantum information:
This model is often used to represent worst-case scenarios in quantum error correction studies [Das20].
Amplitude Damping Noise: This noise model describes energy loss in quantum systems, such as a photon being absorbed or an excited atom decaying to a lower energy state. The amplitude damping process affects the \(|1\rangle\) state:
where \(\gamma\) is the damping probability. Amplitude damping is significant in optical and superconducting qubit systems [Nguyen19].
Dephasing Noise:Dephasing noise affects the relative phase between quantum states without changing the population of the states. It can be modeled as:
where \(\lambda\) is the dephasing rate. Dephasing is a common challenge in maintaining coherence in qubits over time [Andersen20].
Collective Noise: In quantum networks, qubits may experience correlated errors due to shared environmental influences. Collective noise models capture these correlated errors, which can be more challenging to correct because they affect multiple qubits simultaneously [Caro20].
Understanding and characterizing these noise models is vital for developing effective quantum error correction methods. They inform the design of error correction codes and influence the architecture of quantum networks to mitigate the impact of errors.
Having traversed the landscape of quantum errors that plague our delicate qubits, we now stand at the forefront of humanity's ingenious solutions to these challenges. Just as ancient mariners learned to navigate treacherous seas by the stars, researchers have devised remarkable methods to preserve quantum information against the tempestuous environment. In this section, we explore the existing error correction techniques that form the backbone of reliable quantum computing and communication.
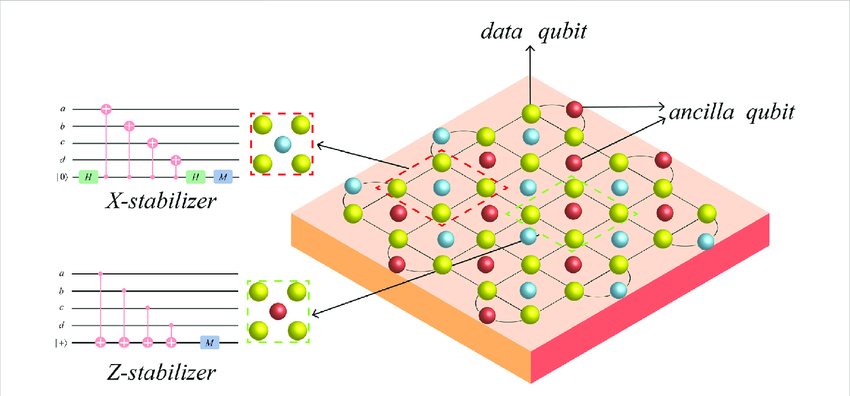
Figure 2 illustrates the lattice structure of a surface code, which is pivotal in topological quantum error correction methods. The surface code arranges qubits on a 2D lattice where quantum information is stored in the global properties of the surface, making it robust against local errors.
Imagine you're sending an important message through a noisy channel. In the classical world, you might repeat the message multiple times to ensure it gets through correctly. Inspired by this idea, early quantum error correction schemes employed redundancy, but with a quantum twist. Since qubits cannot be cloned due to the no-cloning theorem [Wootters82], we can't simply copy them. Instead, we distribute the information of a single qubit across multiple qubits in an entangled state.
The three-qubit bit-flip code is a foundational example. Here, the logical qubit \(|\psi\rangle\) is encoded into three physical qubits:
This encoding allows the detection and correction of a single bit-flip error. However, it doesn't protect against phase-flip errors. To address both bit-flip and phase-flip errors, the Shor code extends this idea by using nine qubits [Shor95].
Enter the realm of stabilizer codes, a powerful framework introduced by Daniel Gottesman [Gottesman96]. Stabilizer codes use the concept of stabilizer operators, which are measurements that leave the encoded quantum state unchanged (i.e., they "stabilize" the state). By measuring these operators, we can detect errors without collapsing the quantum information.
The process involves initializing ancillary qubits and performing entangling operations to extract error syndromes, which indicate the presence and type of errors. This method forms the basis of many quantum error correction codes used today [Terhal15].
As researchers sought more efficient codes, the Calderbank-Shor-Steane (CSS) codes emerged as a significant milestone. Named after their inventors-Calderbank, Shor, and Steane-CSS codes cleverly combine classical linear codes to construct quantum error correction codes [Calderbank96].
The magic of CSS codes lies in their ability to correct both bit-flip and phase-flip errors using two classical codes that satisfy certain duality conditions. Specifically, they use a pair of classical linear codes \( C_1 \) and \( C_2 \), where \( C_2 \subset C_1 \). The quantum code is then constructed by encoding qubits into superpositions of codewords from these classical codes:
Here, \(|\psi\rangle\) represents the logical qubit state, and \( c \) runs over codewords in \( C_2 \). CSS codes are highly practical and have been implemented in various quantum computing platforms [Erhard21].
In the quest for scalable quantum error correction, Quantum Low-Density Parity-Check (QLDPC) codes have gained significant attention. Inspired by their classical counterparts, QLDPC codes feature sparse parity-check matrices, which means each parity check involves only a small number of qubits. This sparsity reduces the complexity of error detection and correction procedures [Gottesman13].
Recent advancements have led to the discovery of QLDPC codes with promising properties, such as constant rate and a fault-tolerance threshold that may surpass that of the popular surface code [Bonilla21]. These codes hold the potential for more efficient quantum error correction in large-scale quantum computers.
Error correction alone isn't enough if the process of correcting errors introduces new errors. This conundrum led to the development of fault-tolerant quantum computation. The goal is to perform quantum operations in a way that prevents errors from cascading and corrupting the computation irreparably [Knill98].
Fault tolerance is achieved through careful design of quantum gates and circuits. For example, transversal gates apply operations across qubits in a way that errors don't spread uncontrollably. Fault-tolerant protocols often use extra qubits and more complex circuits, balancing resource overhead against reliability [Chamberland20].
The threshold theorem states that if the error rate per operation is below a certain threshold, arbitrarily long quantum computations can be performed reliably using fault-tolerant methods. This theorem provides hope that practical quantum computing is achievable despite the fragility of quantum states [Fowler12].
Venturing into the geometrical realm, topological quantum codes harness the properties of topology to protect quantum information. The most prominent example is the surface code, which arranges qubits on a 2D lattice and encodes logical qubits into the global properties of the surface [Kitaev03].
In the surface code, qubits are organized such that errors manifest as localized defects, and error correction involves identifying and neutralizing these defects. The code's robustness comes from the fact that logical errors require large, connected chains of physical errors, which are statistically unlikely [Bonilla20].
Topological codes are highly attractive for their high fault-tolerance thresholds and compatibility with 2D qubit architectures, such as those based on superconducting circuits and trapped ions. Recent experiments have demonstrated the surface code's viability, bringing us closer to realizing fault-tolerant quantum computers [Andersen20].
To further enhance error correction capabilities, concatenated codes layer multiple quantum codes within each other. Imagine a Russian nesting doll, where each doll protects the one inside it. In concatenated coding, a logical qubit is first encoded using one quantum code, and each of the resulting physical qubits is then encoded again using another code [Knill05].
This hierarchical approach exponentially suppresses error rates at the cost of increased qubit overhead and circuit complexity. Concatenated codes are instrumental in theoretical analyses of fault-tolerant thresholds and provide a pathway to achieving the low error rates required for practical quantum computing [Cross15].
Researchers continue to explore optimal combinations of codes and levels of concatenation to balance resource demands with error suppression effectiveness. Advances in this area contribute to the development of scalable quantum architectures [Li19].
Standing at the cusp of a quantum revolution, we find ourselves both exhilarated by the possibilities and humbled by the challenges that lie ahead. The quest to harness quantum mechanics for computing and communication has led us to ingenious solutions, yet the journey is far from over. In this dynamic landscape, researchers are charting new territories, exploring innovative approaches to overcome the limitations of current quantum error correction methods. Let's embark on a voyage through these emerging frontiers, where cutting-edge techniques promise to elevate quantum technologies to unprecedented heights.
Table 2 summarizes some of the most promising emerging techniques in quantum error correction, highlighting their descriptions and advantages.
| Technique | Description | Advantages |
|---|---|---|
| Reinforcement Learning | Uses RL agents to optimize error correction strategies. | Adaptive to changing noise models. |
| Machine Learning | Employs supervised and unsupervised learning for error decoding. | Handles complex error patterns. |
| Software-Based QEC | Error mitigation through software algorithms and post-processing. | Reduces hardware overhead. |
In the subsequent subsections, we delve deeper into each of these techniques, exploring how they contribute to the future of quantum error correction.
Imagine training a dog to fetch a ball-you reward it when it succeeds and encourage it to try again when it fails. This basic principle of learning from interaction and feedback is at the heart of reinforcement learning (RL), a branch of machine learning where agents learn optimal behaviors through trial and error [Sutton18].
In the context of quantum error correction, RL algorithms can be employed to design and optimize error correction strategies without explicit programming. By simulating quantum environments, RL agents can explore vast possibilities of error syndromes and recovery operations, learning to minimize the error rates over time [Nautrup19].
For example, researchers have developed RL-based decoders for surface codes that adapt to changing noise models, outperforming traditional decoding algorithms under certain conditions [Torlai17]. This adaptability is crucial in real-world quantum devices, where noise characteristics can be complex and non-static.
The integration of RL with quantum error correction represents a promising avenue, potentially leading to more robust and efficient error mitigation techniques that can keep pace with the evolving landscape of quantum hardware [Fitzek21].
As quantum systems scale up, the likelihood of errors affecting multiple qubits simultaneously increases. These arbitrary multiple-qubit errors pose significant challenges, as traditional error correction codes are primarily designed to handle single-qubit errors [Hastings20].
To address this, researchers are exploring new mechanisms that can detect and correct errors spanning several qubits. One approach involves developing codes with higher-distance parameters, which can correct more errors but require additional resources [Roffe18].
Another promising direction is the use of entanglement-assisted quantum error correction, where shared entanglement between qubits is leveraged to enhance error detection capabilities [Hsieh05]. Additionally, adaptive error correction protocols that dynamically adjust based on the observed error patterns are being investigated [Krastanov19].
These mechanisms aim to fortify quantum systems against complex error scenarios, ensuring that the integrity of quantum information is maintained even as we push the boundaries of qubit count and operational complexity.
In the realm of classical computing, software plays a pivotal role in managing hardware imperfections. Similarly, software-based quantum error correction seeks to implement error mitigation techniques at the software level, complementing or even reducing the burden on physical error correction codes [Temme17].
Techniques such as quantum error mitigation utilize post-processing algorithms to estimate and subtract the effects of errors from measurement outcomes. For instance, the zero-noise extrapolation method involves executing quantum circuits at varying noise levels and extrapolating results to the zero-noise limit [Li17].
Moreover, software frameworks are being developed to simulate quantum error correction protocols, optimize quantum circuits, and automate the generation of fault-tolerant gate sets [Javadi18]. These tools empower researchers and developers to experiment with error correction strategies without the immediate need for large-scale quantum hardware.
Software-based approaches offer flexibility and rapid iteration, playing a crucial role in the near-term development of quantum technologies, particularly during the era of noisy intermediate-scale quantum (NISQ) devices [Preskill18].
Beyond reinforcement learning, other branches of machine learning are making inroads into quantum error correction. Supervised learning models, such as neural networks, can be trained on labeled datasets of error syndromes and corresponding recovery operations, effectively learning to decode errors [Alsina16].
Unsupervised learning techniques are also being explored to detect patterns in error occurrences without explicit labels. For example, clustering algorithms can identify correlations in error data that may not be apparent through traditional analysis [Varsamopoulos18].
Generative models, like variational autoencoders and generative adversarial networks, have potential applications in simulating quantum noise and generating synthetic training data for ML models [Ng09].
The synergy between ML and quantum error correction holds promise for creating more adaptive and intelligent error management systems, capable of handling the complexities of real-world quantum devices.
The final piece of the puzzle lies in the seamless integration of error correction methods with quantum hardware. As quantum processors evolve, tailoring error correction strategies to the specific characteristics of the hardware becomes essential [Corcoles20].
Researchers are working on hardware-aware optimization, where error correction codes and protocols are designed with the hardware's noise profile, connectivity, and operational constraints in mind. For instance, customizing the placement of qubits and the routing of quantum gates can minimize error rates [Stricker21].
Advances in quantum firmware are enabling more efficient execution of error correction routines, with low-level control over qubit operations and real-time error monitoring [Kelly15].
Collaborative efforts between hardware engineers and quantum information scientists are crucial for this integration. By aligning error correction techniques closely with hardware capabilities, we can enhance performance and accelerate the path toward practical quantum computing.
Our journey through the realm of quantum error correction in hybrid quantum-classical networks has unveiled a landscape rich with challenges and innovations. From understanding the fundamental nature of quantum errors to exploring sophisticated error correction codes and envisioning future directions, we stand at the forefront of a transformative era.
The interplay between quantum and classical systems offers a pathway to harnessing quantum mechanics' full potential. Yet, the fragility of quantum information necessitates relentless pursuit of advanced error correction methods. As we have seen, researchers are not only refining existing techniques but also pioneering new approaches that leverage machine learning, software innovations, and hardware integration.
The road ahead is undoubtedly arduous, but the rewards are profound. By overcoming the barriers posed by quantum errors, we inch closer to realizing powerful quantum computers and secure quantum communication networks. The collaborative spirit and interdisciplinary efforts in this field inspire optimism that the quantum dreams of today will become the technological realities of tomorrow.
Continued research, investment, and innovation are essential. As we advance, each discovery builds upon the last, illuminating the path forward. The story of quantum error correction is still being written, and its chapters hold the promise of unlocking mysteries and capabilities beyond our current imagination.