| Jinhao Zhao, jinhaoz@wustl.edu (A paper written under the guidance of Prof. Raj Jain) |
Download |
Quantum communication is based on quantum informatics. Due to the no-cloning theorem, the best usage is for designing a secure way to transmit information. The most effective way is using quantum channels to generate secret keys. However, the experiments show that the distance of quantum channels is still limited; also, implementing the quantum algorithms with high correctness is still a hard question. Even with these limitations, there are several recent advances in this area.
Quantum Communication, Quantum Key Distribution, Quantum Mechanics
2.1 Definition and Analysis of Qubits
3 Protocols for Quantum Communications
4.1 Links based on OAM and LG modes
Quantum Communication is defined as teleporting messages through quantum carriers or tunnels. It is a subarea for quantum informatics, so many results and definitions interact.
As an interdisciplinary area, quantum communication consists of physics and computer science. Also, it is both theoretical and practical. Constructing a quantum communication system requires a complete theory and a stable tunnel simultaneously. Therefore, the analysis of quantum communication should be separated into two parts: theories and experiments.
A very common misunderstanding (the counterpart also common sense in related areas) is that quantum communication could transfer information instantly through very far distances, as shown in many science fictions. This is wrong. According to results from physics, no information could travel faster than light. The main usage for quantum communication is for security affairs, which could generate a solid communication system that seems impossible to hack. The theoretical part of quantum communication is for designing the protocols, and the idea is for enhancing security, while reducing the resources, like entangled qubits.
However, the experimental result is very poor compared with the theoretical part, is also the challenge of quantum communication. Firstly, the stability of multiple qubits is bad. Even in laboratories, there could only be a few qubits that are entangled, but some protocols require arbitrarily large; it may take a century to achieve this scheme. Secondly, the entanglement through long distances is easy to break, usually because there are tons of disturbs in the tunnel. Although there are good results in the news, it has a far distance to an available tunnel.
To be friendly to readers, we will show how quantum communication works from the very beginning. It may not be so rigorous, so we encourage interested readers to have a look at formal productions. Then, we will introduce several quantum protocols, which enhance the sense of security. Finally, we list some recent advances in quantum communication.
In this section, we will show some key concepts of quantum information, which is the basis of quantum communication.
In this subsection, we will start with the definition of qubit and cast analysis on it.
Qubit is an informatic concept. It is usually represented by photons, just like normal bits are recorded in a disk. As the simplest example, if there are two possible ways for a photon to take, then this information is a qubit.
We use Bra-ket Notation to represent a qubit. Denote the two possible ways as |0⟩ and |1⟩, here are its advantages:
- In experiments from physicians, the photon could be "both in the two ways". This could be represented as 1/√2|0⟩ + 1/√2|1⟩ in the system. We also have a short notation as |+⟩.
- If we want to measure the qubit, it may return in probabilities. Assume ⟨a|b⟩ means the result for measuring whether |b⟩ is |a⟩, then ⟨0|0⟩=1 (because it is always on its way), ⟨1|0⟩=0, and ⟨+|0⟩=1/2. Here |a⟩ and its counterpart is called a basis.
A mathematical way to think of qubits is to take it as a vector. Let |a⟩=x|0⟩+y|1⟩, it could also be written as (x,y)T. Here x and y could be complex numbers, where the additional dimension is to show the polarization of the photon (in fact, usually we denote polarization by the difference of |0⟩ and |1⟩, and y's imaginary part is for whichever way it takes). We know that the measurements could be represented as inner production.
Now we have some knowledge about a single qubit, then we will show about multiple qubits.
When there are multiple qubits, they may or may not be entangled. This could be handled by mathematical analysis.
The Bra-ket way to encode multiple qubits is simply writing them continuously. Two qubits |0⟩|0⟩ could be written as |00⟩. Of course, it is not entangled because we could write the two bits separately.
A universal and mathematical way is the Cartesian product. If |a⟩=(x1,y1)T, |b⟩=(x2,y2)T, then |ab⟩=(x1,y1)T × (x2,y2)T=(x1x2,x1y2,y1x2,y1y2)T. This is similar to the one qubit notation, since (a,b,c,d)T = a|00⟩+b|01⟩+c|10⟩+d|11⟩.
Intuitively, if the two qubits (a,b,c,d) could be decomposed as (x1,y1)T × (x2,y2)T, then it is not entangled; if it could not, then it is entangled. This is correct, and there is proof about it, which is too long to show it here.
For example, (1/2,1/2,1/2,1/2) is not entangled, since it could be decomposed as (1/√2,1/√2)×(1/√2,1/√2), which is also |++⟩.
But (1/√2,0,0,1/√2)=1/√2|00⟩+1/√2|11⟩ could never be decomposed. This is called an EPR pair. If we measure the two qubits one by one in an EPR (Einstein–Podolsky–Rosen) pair, then the first result is arbitrary, but the second result must be the same as the first result.
Many properties of quantum communication come from entanglement. To make it complete, we provide another property.
Just like normal bits having a NOT gate, qubits also have quantum gates to change their position.
A quantum gate could be defined as a unitary matrix. For example, a NOT gate for a qubit switches its two axes, which is also called X. There are also other single-qubit quantum gates, like Z, Y and H.
A quantum gate could also cast on multiple qubits. The idea of the XOR gate in normal bits comes to the CNOT (Controlled-NOT) gate, where CNOT(|0a⟩+|1a⟩)=|0a⟩+|1⟩NOT|a⟩. It could be examined in the mathematical form that it has all the properties as described.
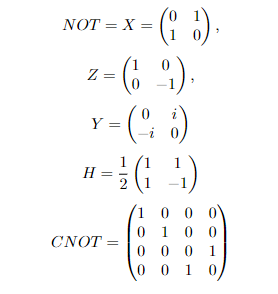
Figure 1 Some quantum gates
The quantum gate could model all the operations cast on the qubits. However, from mathematics, we could prove that there are functions that cannot be interpreted by quantum gates, which means they are also not likely to achieve in the real world. For example, cloning an arbitrary qubit is impossible through quantum gates, which is also called the no-cloning theorem. This may be the main inspiration for applying quantum informatics to security areas.
Now we have finished all our preparations. Let's see how far we will reach with this (quite simple in quantum information) system!
In this section, we will show some famous protocols in quantum communications.
Superdense coding is a protocol that it transfers a few qubits based on pre-generated shared entangled states, and in this way, it could send more information in bits. In detail, it consists of the following steps:
Table 1 Protocol for Superdense Coding
1. Alice and bob generate entangled states, and they keep their part.
2. Now Alice wants to send some information. She casts some quantum gates on her qubits (encoding).
3. Alice sends her qubits to Bob through a quantum channel.
4. Bob gets the full entangled states. He casts some quantum gates on the full states (decoding) and reads the result.
The simplest example is that Alice and Bob share the EPR pair 1/√2|00⟩+1/√2|11⟩. Alice could send 2 bits by just sending one qubit. She would do the following:
Table 2 Quantum gates for 2-bit Superdense Coding
a) If Alice wants to send 00, then she casts I (nothing) on her qubit.
b) If Alice wants to send 01, then she casts X (as defined in section 2.3) on her qubit.
c) If Alice wants to send 10, then she casts Z on her qubit.
d) If Alice wants to send 11, then she casts Y on her qubit.
After Bob receives Alice's qubit, he casts CNOT on the state, and then casts H on the first bit.
Take case b) as an example. The quantum state after each step is
Table 3 Example for a 2-bit Superdense Coding
Step 1 EPR pair: 1/√2|00⟩+1/√2|11⟩
Step 2 X: 1/√2|10⟩+1/√2|01⟩
Step 3 send: the same
Step 4 CNOT: 1/√2|11⟩+1/√2|01⟩
Step 4 H: |01⟩, which is exactly what Alice wants to send.
This protocol requires a quantum channel and pre-generated entangled states. It has a sense of security because if the attacker gets the qubit sent in step 3, he has no idea about the message. However, this protocol only uses quantum channels. If traditional channels are used, things may get much more efficient.
The idea for combining the quantum channel and the traditional channel is called quantum key distribution (QKD), in which the quantum channel is used for generating secret keys, and the message is sent by the traditional channel based on cryptography. BB84 is a QKD protocol that only produces a key.
The protocol has the following steps:
Table 4 Protocol for BB84
1. Alice generates a sequence of qubits randomly, each one of |0⟩, |1⟩, |+⟩, |-⟩. (Recall |+⟩=1/√2|0⟩ + 1/√2|1⟩, and |-⟩=1/√2|0⟩ - 1/√2|1⟩). She transfers the sequence to Bob via a quantum channel.
2. Bob measures the states randomly in basis (|0⟩, |1⟩) or basis (|+⟩, |-⟩. According to the definition of measurement, the result is as Table 5.
3. Alice and Bob recall every choice is in either (|0⟩,|1⟩) or (|+⟩, |-⟩), and share this information via a traditional channel.
4. For each bit, if their choices are in the same group, then Bob has received the key by treating |0⟩ and |+⟩ be 0, while |1⟩ and |-⟩ be 1; if their choices are in different groups, then this bit is ignored. The probability of they are in the same group is 50%, so half of the bits could be used as a key.
Table 5 Results in BB84 protocol. Each column is the bit that Alice sent, and each row is Bob's basis.
| Bob\Alice | |0⟩ | |1⟩ | |+⟩ | |-⟩ |
|---|---|---|---|---|
| (|0⟩,|1⟩) | |0⟩ | |1⟩ | 50% of |0⟩ and |1⟩ | 50% of |0⟩ and |1⟩ |
| (|+⟩,|-⟩) | 100% | 85% | 50% of |+⟩ and |-⟩ | 50% of |+⟩ and |-⟩ |
The security of BB84 is because the traditional channel (step 3) consists of no information. To get information, the attacker must cast measurements on the qubits, which will change the quantum state. Alice and Bob could reveal a short part of their keys, and check whether it is the same. If not, it means an attacker has measured the qubits.
BB84 only requires a quantum channel. Also, there are some QKD protocols only require entangled states.
E91 is a protocol that only requires entangled states. It is more complicated in calculations, so we only introduce a sketch. It includes the following steps:
Table 6 Protocol for E91
1. Alice and Bob generate several EPR pairs in advance, and each keeps one bit in the pair.
2. Alice and Bob separately measure their bits in one of three bases.
3. They show which basis in each step they have used via a traditional channel. If the bases they used are resulting in a 100% probability for agreement, then they have got a shared bit for the key; if it is not 100%, then this bit is ignored.
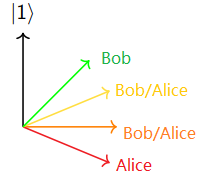
Figure 2 How E91 gets an agreement[1] . If Alice and Bob are on a different basis, the probability of agreement follows a certain formula, i.e., Bell's Theorem
The bases are constructed subtly, so when the bases are different on the bit, the probability for whether their qubits are the same is a certain value as the following table.
Table 7 Percentages for the agreement in E91 protocol. Each column is Alice's basis, and each row is Bob's basis.
| Bob\Alice | Basis 1 | Basis 2 | Basis 3 |
|---|---|---|---|
| Basis 1 | 85% | 50% | 15% |
| Basis 2 | 100% | 85% | 50% |
| Basis 3 | 85% | 100% | 85% |
The deprecated bits could be used for detecting the attacker. Alice and Bob can reveal these bits and check the statistics. If it is far away from the expectation, then the attacker is sure to exist.
QKD protocols, including BB84 and E91, are totally for security affairs. Its application area is the same as traditional cryptography, like RSA[2], but RSA's security comes from factoring an integer, which is also proved to be weak under quantum computers, so it is not safe in the future. We do not have quantum computers, but we could indeed cast BB84 in today's technology. Most experiments are designed for these QKD protocols.
The challenges for implementing quantum channels are that there must be little disturbance, since any noise may change the state of the quantum, making it collapse or disentangle. Unfortunately, keeping the quantum entangled is even harder by experiments, especially when it is far away. Therefore, experiments are usually designed for BB84-like protocols, which require sending a sequence of quantum.
As we have discussed, quantum states are based on the properties of lights. Orbital Angular Momentum (OAM) is the most popular property for lights, which is determined by the angular momentum of light.
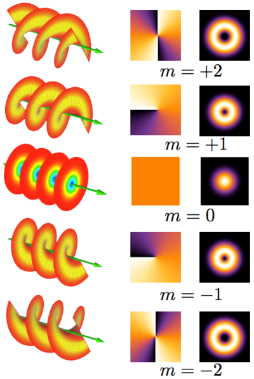
Figure 3: Visible OAM modes, where m is a factor in the mode[3]
Also, there are other properties in the light beam to extract. Usually, Laguerre-Gaussian (LG) beams are used for experiments, so LG modes is also useful, which is derived from solving the paraxial Helmholtz equation. In LG modes, the OAM could be a constant or even zero.
Photons could be transmitted and collected through free spaces, but according to their complex environment, the distance is strictly limited to get a correct result. A remarkable result is that in Ottawa, scientists have built a free-space link between the rooftops of two buildings, with a distance of about 300m. Note that in this kind of distance and free spaces, we usually use LG modes, but OAM modes could also be used and tested.
If the quantum state is not generated from LG beams, there could be other modes, like space and time. This happens on fibers, and it is so familiar since it has already been used by today's internet.
Recent results mainly strengthen the distance, including expanding the maximum distance and increasing the stability in the fair distance. Results in the fiber-based links vary from 1km to 100km. In the 1km case, it could be multicore, which means it is bidirectional and has higher reliability. It could also mix with other modes like OAM to get a higher dimension of the quantum states. The correct rate within these cases is about 80% to 90%[Daniele21], which is enough for protocols like BB84. When the distance comes to 100km, it could only be stable for a single core. It may have higher channel loss, but it could still transmit with a high data rate.
As a result, although we have good results based on different media, it is still too short for a useful system in the real world. There is a long way to go to improve the correctness and enlarge the distance while making the whole system stable.
We have gone through the basic definition of qubits, entanglement, and quantum mechanics, showing that quantum communication is not a mysterious area. Also, we have a brief view of several quantum protocols, which are simple in the definition. Although more and more protocols are designed, it is very hard to implement a stable quantum channel. The biggest challenge is to make the distance larger, for example, being able to send from the earth to the artificial satellite. If there is a possible way to do this, since transmission in outer space is not likely to be disturbed, we could make use of the quantum protocols. The techniques are based on materials and discoveries in physics, so new results are continuing to arise.
1. Daniele Cozzolino, Beatrice Da Lio, Davide Bacco, "High‐dimensional quantum communication: benefits, progress, and future challenges", in Advanced Quantum Technologies, vol. 2, issue 12, December 2019. https://doi.org/10.1002/qute.201900038
2. Ilan Kremer, "Quantum communication". March 1995. DOI:10.1007/3-540-44678-8_3
3. Ronaldde Wolf, "Quantum communication and complexity", in Theoretical Computer Science, vol. 287, issue 1, pp. 337-353, September 2002. https://doi.org/10.1016/S0304-3975(02)00377-8
4. Yu-Ao Chen, Qiang Zhang, Teng-Yun Chen, etc. "An integrated space-to-ground quantum communication network over 4,600 kilometres", in Nature, vol. 589, pp. 214–219. January 2021. https://www.nature.com/articles/s41586-020-03093-8
5. Mario Mastriani, Sundaraja Sitharama Iyengar & Latesh Kumar, "Satellite quantum communication protocol regardless of the weather", in Opt Quant Electron, vol. 53, p. 181, March 2021. https://link.springer.com/article/10.1007/s11082-021-02829-8
6. Sumeet Khatri, Mark M. Wilde, "Principles of Quantum Communication Theory: A Modern Approach", arXiv:2011.04672. https://arxiv.org/abs/2011.04672
7. Xiao-Min Hu, Cen-Xiao Huang, Yu-Bo Sheng, etc., Guang-Can Guo, "Long-Distance Entanglement Purification for Quantum Communication", in Physical Review Letters, vol.126, issue 1-8, January 2021. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.010503
8. N. Hosseinidehaj, Z. Babar, R. Malaney, S. X. Ng and L. Hanzo, "Satellite-Based Continuous-Variable Quantum Communications: State-of-the-Art and a Predictive Outlook", in IEEE Communications Surveys & Tutorials, vol. 21, no. 1, pp. 881-919, August 2018. https://ieeexplore.ieee.org/document/8439931
9. Giulio Chiribella, Manik Banik, Some Sankar Bhattacharya, etc., "Indefinite causal order enables perfect quantum communication with zero capacity channels", in New J. Phys, vol. 23, March 2021. https://iopscience.iop.org/article/10.1088/1367-2630/abe7a0/meta
10. Sergienko, Alexander V., etc. "Quantum communications and cryptography". CRC press, October 2018. ISBN 9780367391744
11. Yousefjani, Rozhin, and Abolfazl Bayat. "Parallel entangling gate operations and two-way quantum communication in spin chains", in Quantum, vol. 5, p. 460, May 2021. https://quantum-journal.org/papers/q-2021-05-26-460/
| BB84 | Quantum protocol designed by Charles Bennett and Gilles Brassard in 1984 |
|---|---|
| CNOT | Controlled-NOT (gate) |
| E91 | Quantum protocol designed by Artur Ekert in 1991 |
| EPR | Einstein–Podolsky–Rosen (pair), also known as Bell State. |
| LG | Laguerre-Gaussian (beam) |
| OAM | Orbital Angular Momentum |
| QKD | Quantum Key Distribution |
| RSA | Traditional cryptography protocol designed by Rivest, Shamir and Adleman |
| XOR | exclusive-OR (gate) |
[1] Modified from lecture slides on Introduction to Quantum Computing.
[2] A famous traditional protocol in cryptography with asymmetric keys. It is still widely used in today's Internet for security.
[3] From Wikipedia.
Last modified on December 7, 2022
This and other papers on recent advances in Wireless and Mobile Networking are available online at http://www.cse.wustl.edu/~jain/cse574-16/index.html
Back to Raj Jain's Home Page