CSE131: Procedural Abstraction

Let's continue our discussion on computing the area of a circle. We saw that using a named constant PI and a radius variable r helped, since we don't have to continually write out the value of Pi.

However, we still had to keep writing the formula over and over. For example, we have to say r * r every time we want to square the radius, and then we have to remember to multiply by Pi.

Let's first address the problem of squaring a number. Instead of having to write the expression r * r every time, it would be nice to have a black box, or a procedure, that would take in a numerical argument and return the square of that argument.

If we had this, we could write

square(837)

instead of 837 * 837. This may not save us much typing but one can argue that the code is more readable, and certainly if we were taking cubes or higher powers, it would become ridiculous to start stringing the numbers all out in a line.

In Java, we can create a procedure called square as follows:

double square(double x) {
  return (x * x);
}

The "double" at the beginning is the type of return value from the procedure. This is followed by the name of the procedure, and then a list of formal parameters separated by commas. In this case, there is only one formal parameter, called x and its type is double.

When the procedure is invoked, the actual values passed in from the procedure call are bound to the formal parameters. The part in curly braces ({}) is the procedure body. The procedure body contains some number of statements that are executed in order. When one of the formal parameters is used inside the body, it's value is the value that was passed in from the calling procedure. The expression in the return statement is evaluated at the end of the execution of the procedure and the resulting value is returned to the calling procedure as the value of the procedure call.

Now let's invoke the procedure. Suppose we execute the line

double area3 = square(3);

The value 3 is called the actual parameter to which the formal parameter x will be bound. Java creates a little binding table

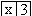for use inside the procedure and then evaluates the procedure body using that binding table. This little binding table is called an environment.

So, the actual parameter 3 is passed into the procedure square and bound to the variable x. Then the body of the procedure is executed. The return value 9 is computed, returned as the value of the expression "square(3)", and subsequently assigned to the variable area3.

Any expressions can be used in the actual parameter list when making a procedure call, provided that the types match the types of the corresponding formal parameter list. For example,

double x, y;
double r = 3;

x = square(2+1);    // 2 + 1 is evaluated, 3 is passed in
y = square(r);      // r is evaluated, 3 is passed in
i = square("3");    // ERROR: type String doesn't match double parameter

Example: areaOfCircle

Having a square procedure is fine, but what we really want is a procedure called areaOfCircle that compute the area of a circle, given the radius. Then we could write statements like

double area5 = areaOfCircle(5);

So, how do we write the procedure? Assuming that we have already defined the constant PI, we can write:

double areaOfCircle(double radius) {
  return (PI * square(radius));
}

Notice that we are using the square procedure to compute the square of the radius.

Let's do some more examples of procedures.

Example: hypotenuse

Suppose we are given a procedure sqrt that takes one parameter (a double) and returns its square root:

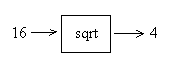
We don't know what sqrt is doing inside, but we can use it anyway because we understand its specification. This is a nice advantage of procedural abstraction.

Suppose we want a procedure hyp that finds the length of the hypotenuse of a right triangle, given the lengths of the other two sides.

Recalling that the length of the hypotenuse is the squre root of the sum of the squares of the lengths of the sides, we can write:

double hypotenuse(double sideA, double sideB) {
  return sqrt(square(sideA) + square(sideB));
}

And we can call the procedure as follows:

double hyp = hypotenuse(3,4);

Let's think about the evaluation step by step, using the substitution model:

hypotenuse(3,4)
sqrt(square(3) + square(4))
sqrt((3 * 3) + (4 * 4))
sqrt(9 + 16)
sqrt(25)
5

Built-in Mathematical Procedures

To get all of this to work, we need a procedure for square root. We could write one, but Java provides a lot of standard mathematical functions as methods of a static class called Math. (A method is a procedure defined as part of a class.)

We'll say more about classes later, but for now you can think of the math class as a collection of procedures (methods) and constants, accessed by Math.name-of-method or Math.name-of-constant. Examples include:

Math.sqrt(double x)    // returns the square root of x
Math.pow(x,y)          // returns x raised to the power y
Math.PI                // an approximation of pi

See the Math class documentation for a complete list of the available methods and constants.

Another useful class is the System class that provides an output stream for printing textual output from your program to the screen, as in the following example.

A Complete Program

Let's write a complete program using the procedures we have created. The program calculates hypotenuses of some right triangles.

public class Triangles {
   public static void main(String args[]) {
      test(3,4);
      test(9,12);
   }

   public static double square(double x) {
      return (x * x);
   }

   public static double hypotenuse(double sideA, double sideB) {
      return Math.sqrt(square(sideA) + square(sideB));
   }

   public static void test(double a, double b) {
      System.out.print("A right triangle with sides " + a + " and " + b);
      System.out.println(" has hypotenuse " + hypotenuse(a,b));
   }
}

Some notes:

The first line says that we are defining a class called Triangles that is publicly available (accessible externally).
The second line sets up a method called main that will be the entry point of the program.
The modifier static means that the method is part of the class, as opposed to a method of an object instance of the class. We'll see more about this later, but for now, just think of a class as a type of object. We may create many objects of a given class and call methods on those objects to ask the objects to do things. However, sometimes we want the class itself to be able to do things. These are called static methods.)
The modifier void means that the method does not return a result.
The System.out.print method prints its argument to the screen. The System.out.println method is the same, except that it also goes to the next line after printing.

So, the output of the program would be:

A right triangle with sides 3 and 4 has hypotenuse 5.
A right triangle with sides 9 and 12 has hypotenuse 15.

Advantages of Procedural Abstraction

To conclude, here are some advantages of procedural abstraction.

Hides details.
Allows us to think about the general framework & postpone details for later.
Gives us building blocks we can reuse in other situations.
Lets us use local names.
Lets us easily replace implementations by better ones.

Reduction

Suppose we want to find the diagonal of a rectangle with sides a and b. The procedure could be written as

double rect_diag(double s) {
  return Math.sqrt(square(a) + square(b));
}

However, we can save ourselves some work by using what we've already done. We can reduce the problem of finding the length of the diagonal of a rectangle to the problem of finding the hypotenuse of a right triangle, as shown in the following diagram.

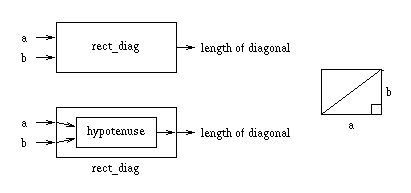
This would be coded as

double rect_diag(double a, double b) {
  return hypotenuse(a, b);
}

We've transformed one problem to another. This is called a reduction. This is useful in many areas of computer science.

Conditional statements

Let's do another example of procedural abstraction. Suppose that Math.abs wasn't built in. Thus, we want a black box like this:

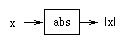
The mathematical definition of this function is

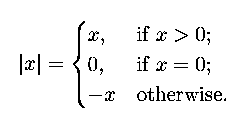
double abs(double x) {
  return ???

Wait! How can we do something different depending on the value of x? So far, all of our computations have been uniform -- they do the same thing to every input, regardless of its value.

What we want is for the execution to be conditional on some test. For the test, we can use any boolean expression (also known as a predicate). But how do we make the execution conditional on whether the test is true or false?

For this purpose, Java provides conditional statements. One possible form is

if condition    // NO SEMICOLON!!
  consequent;

Here, the consequent is executed iff (if and only if) the condition is true. The other possible form is

if condition
  consequent1;
else
  consequent2;

Here, if the condition is true, then consequent1 is executed; otherwise, consequent2 is executed.

Using this construct, the abs example could be written as

double abs(double x) {
  if (x > 0)
    return x;
  else if (x == 0)
    return 0;
  else
    return -x;
}

We can shorten this a bit, but it's important to check that all possible cases are covered!

double abs(double x) {
  if (x >= 0)
    return x;
  else
    return -x;
}

Notice that execution continues after the conditional statement, so we could also have written

double abs(double x) {
  if (x >= 0)
    return x;
  return -x;
}

Note: indentation has no meaning in Java. It is only used for readability.

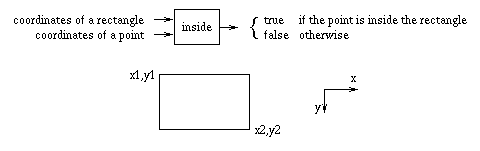
Using the return values from procedures as tests

The test in a conditional statement can be a simple expression or the result of a procedure, as long as it is a boolean expression. Consider

boolean inside(int x1, int y1, int x2, int y2, int px, int py) {
  return ((px >= x1) && (px <= x2) && (py >= y1) && (py <= y2));
}

Now we can use this procedure as a test in a conditional statement. For example,

if inside(3, 3, 10, 12, 5, 7) // rectangle: 3,3,10,12; point: 5,7
  System.out.println("The point is inside the rectangle.");
else
  System.out.println("The point is outside the rectangle.");

We can also use the results of procedures within boolean expressions. This is often useful in tests in conditional statements.

if (hypotenuse(3, 4) != 5)
  System.out.println("Error in hypotenuse test.");

Good and bad style in writing conditional statements

When the consequent has more than one statement, you must use curly braces. When there is only one statement in the consequent, you may omit the curly braces, but some editors expect the braces anyway in order to do automatic indentation of your code.
```
if ... {
  ---;
  ---;
}
else {
  ---;
  ---;
}
```
Always use indentation within the conditional to make the blocks of code more readable and to make it easier to follow control flow.
Try to use simple expressions in your tests. Ideally, the code should make sense when read as an English sentence.
- Good: if (y > Math.sqrt(z)) ...;
- Bad: if !(y < Math.sqrt(z)) ...;
Avoid using a conditional just to return the value of a test. That is, instead of
```
if (exp)
  return true;
else
  return false;
```
write
```
return exp;
```