Just as procedural abstraction lets us think about a series of computational steps as an abstract unit, data abstraction lets us think about collections of data as abstract entities. This is useful for:
An abstract data type (ADT) consists of:
| Interface: | create, deposit, withdraw, transfer |
| Legal behaviors: | any deposit is OK, but withdrawals and
transfers must have sufficient funds deposits and withdrawals accumulate over time |
| Internal representation: | balance |
| Representation invariant: | balance >= 0 |
Does this hold for our implementation? What about a negative balance?
Sphere object
| Interface: | create, move, resize, check if a point is within sphere, volume |
| Legal behaviors: | any position is OK, most recent position is used resize OK as long as r>=0 |
| Internal representation: | x, y, z (center) and r (radius) |
| Representation invariant: | r >= 0 |
resize; recall that
resize is the only way to set the radius.
CS101CanvasCS101Canvas as a way to draw graphics
objects on the screen, put up textual messages, and get user
input.
The CS101Canvas is an implementation of a
graphics display window ADT. In order to use it, you will not
need to understand (or even look at) the internal
implementation. You'll only need to understand the interface
and the associated behaviors.
When you instantiate the CS101Canvas, you get
something that might look like this (the actual appearance
depends on what type of machine you use):
CS101Canvas screen = new CS101Canvas();
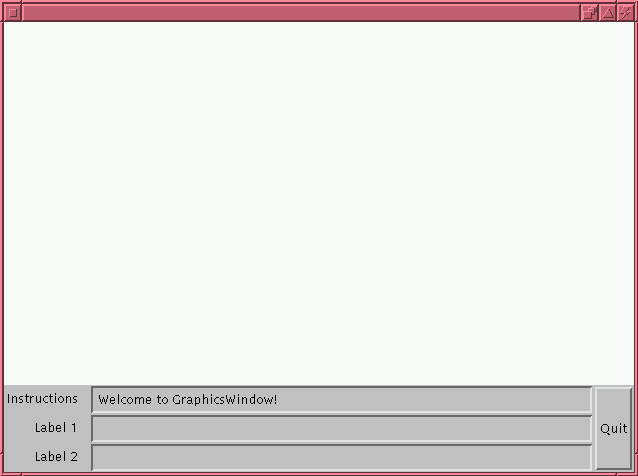
The interface to the CS101Canvas class includes
the following methods:
add(g) -- adds a graphics object
g such as a Rect, Line,
Oval, Text, etc.
remove(g) -- removes graphics object
g from the graphics area
setInstruction(s) -- displays String
s in the instruction text area
setLabel1(s) -- sets the label for the middle
text area to String s
setLabel2(s) -- sets the label for the bottom
text area to String s
setLabelText1(s), setLabelText2(s) -- display
String s in the middle or bottom text area,
respectively
Position click() -- waits for the user to click a
mouse button in the graphics area and returns the position
of the mouse
int getWidth() -- returns the width of the
drawing area as a Rectangle object.
int getHeight() -- returns the height of the
drawing area as a Rectangle object.
sleep(t) -- causes a delay of t
milliseconds, useful for controlling the speed of animations
click() returns only after the mouse button is
clicked in the graphics area.CS101Canvas comes along.
| Method | Parameters | Mutates | Returns |
| constructor | team names | stores team names and initializes all counts | |
hit |
reset count (balls and strikes) for new batter | ||
ball |
increment balls; if 4, walk | ||
strike |
increment strikes; if 3, batter out | ||
foul |
strike if less than 2 strikes so far | ||
walk |
reset count for new batter | ||
batterOut |
reset count and record an out | ||
out |
increment outs; if 3, start a new half inning | ||
run |
increment current team's score (home if bottom of inning or visitors if top) | ||
toString |
description of game status |
Notice that some things are done several times or involve significant work, such as resetting the count or going to a new half. We will create internal (non-public) methods for these.
public class Scorekeeper {
String homeTeam, visitingTeam;
int inning;
boolean topOfInning;
int home, visitors; // score
int balls, strikes, outs; // count
boolean gameOver;
Scorekeeper(String homeTeam, String visitingTeam) {
this.homeTeam = homeTeam;
this.visitingTeam = visitingTeam;
inning = 1;
topOfInning = true;
home = visitors = balls = strikes = outs = 0;
gameOver = false;
}
void resetBallsAndStrikes() {
balls = strikes = 0;
}
public void hit() {
resetBallsAndStrikes();
}
public void ball() {
balls++;
if (balls == 4)
walk();
}
public void strike() {
strikes++;
if (strikes == 3)
batterOut();
}
public void foul() {
if (strikes < 2)
strike();
}
public void walk() {
resetBallsAndStrikes();
}
public void batterOut() {
resetBallsAndStrikes();
out();
}
public void out() {
outs++;
if (outs == 3)
newHalf();
}
public void run() {
if (topOfInning)
visitors++;
else {
home++;
gameOver = ((inning >= 9) && (home > visitors));
}
}
void newHalf() {
resetBallsAndStrikes();
outs = 0;
if ((inning > 8) && (topOfInning == false) && (home != visitors))
gameOver = true;
else {
if (!topOfInning)
inning++;
topOfInning == !topOfInning;
}
}
public String toString() {
if gameOver
return ("Final Score after " + inning + " innings: " + score());
else {
String topBot;
if topOfInning
topBot = "top"
else
topBot = "bottom"
return ("In the " + topBot + " of inning " + inning + "with " +
balls + " balls, " + strikes + " strikes, and "
+ outs + " outs, it's " + score());
}
}
String score() {
if (home > visitors)
return (homeTeam + " over " + visitingTeam + ", "
+ home + " to " + visitors + ".");
else if (visitors > home)
return (visitingTeam + " over " + homeTeam + ", "
+ visitors + " to " + home + ".");
else
return (visitingTeam + " and " + homeTeam + " tied "
+ home + " to " + visitors + ".");
}
}
Notice that some methods are not public (for internal use
only). Also notice several examples of reduction; for
example, hit and walk both use
resetCount.Notice several cases where we use other methods conditionally:
batterOut is called.
walk is called.
Notice that nearly all the methods return void --
they are strictly mutators. In this object, all information
is gained using the toString method. If this
code were embedded in a hand-held umpire's device, some of the
state information (values of instance variables) might be
displayed using LCDs.
Example: Rational Number ADT
Let's look at another ADT example. In this example, a typical
program using the ADT would create many instances of the
class, not just one object, and many of the methods of this
class will create new instances of the class.
We could implement a simple class that holds a pair of integers. The instance variables could be public, meaning that we can access them directly without using a method call.
public class IntPair {
public int a;
public int b;
public IntPair(int a, int b) {
this.a = a;
this.b = b;
}
public String to String() {
return ("(" + a + "," + b + ")");
}
}
Example use:
IntPair p1 = new IntPair(3, 4);
p1.a = 6; // External assignment to public instance variable
Terminal.println("Pair p1 contains " + p1);
The output from the last line would be "Pair p1 contains
(6,4)".
We could store the numerator and denominator of a rational
number in a and b. However, this is
NOT an ADT -- it's just a type of compound data object
that could be used to hold some values and treated as a single
entity.
We could use an IntPair to represent a rational
number like 3/4 by assigning a=3 and
b=4, but we would like to be able to operate on
rational numbers at a higher level. For example, we'd like an
add operation that would sum two rational numbers
to produce a new rational number.
Let's design an interface for our rational number ADT:
| Method | Parameters | Mutates | Returns |
| constructor | numer, denom |
stores numerator and denominator | object reference |
getNumer |
value of numerator | ||
getDenom |
value of denominator | ||
plus |
Rational r |
new Rational: sum of this and
the given parameter r | |
minus |
Rational r |
new Rational: this -
r | |
times |
Rational r |
new Rational: this *
r | |
over |
Rational r |
new Rational: this /
r | |
negate |
new Rational: -this | ||
invert |
new Rational: 1 /
this | ||
toString |
a String of the form numer/denom |
Note that we never change the value of the rational number once it's constructed. Most methods return new rational numbers.
Before proceeding with the implementation, recall:
public class Rational {
int n; // numerator
int d; // denominator
Rational(int numerator, int denominator) {
n = numerator;
d = denominator;
}
public int getNumer() {
return n;
}
public int getDenom() {
return d;
}
public Rational plus(Rational r2) {
int n2 = r2.getNumer;
int d2 = r2.getDenom;
return(new Rational(n*d2 + n2*d, d*d2));
}
public Rational minus(Rational r2) {
return plus(r2.negate());
}
public Rational times(Rational r2) {
int n2 = r2.getNumer;
int d2 = r2.getDenom;
return(new Rational(n*n2, d*d2));
}
public Rational over(Rational r2) {
return times(r2.invert());
}
public Rational negate() {
return (new Rational(-n, d));
}
public Rational invert() {
return (new Rational(d, n));
}
public String toString() {
return ("" + n + "/" + d);
}
}
Example uses of the Rational number class:
Rational oneHalf = new Rational(1, 2);
Rational threeFourths = new Rational(3, 4);
Terminal.println("Adding " + oneHalf + " and " + threeFourths + ":");
Terminal.println("The result is " + oneHalf.plus(threeFourths));
Terminal.println("Now, subtraction:");
Terminal.println(oneHalf.minus(threeFourths).toString());
Terminal.println("Multiplication:");
Terminal.println(oneHalf.times(threeFourths));
Terminal.println("Division:");
Terminal.println(oneHalf.over(threeFourths));
The output is:
Adding 1/2 and 3/4:
The result is 10/8
Now subtraction:
-2/8
Multiplication:
3/8
Division:
4/6
Notice that the fractions are not reduced. After a while, this
could get out of hand. How can we fix this?One possible solutions is to divide the numerator and denominator by the GCD inside the constructor. But how can we compute the GCD? More about this later...