

Objective
In this exercise the students will (1) operate a tube-in-shell heat
exchanger and (2) analyze heat- exchanger performance by the LMTD and  -NTU
methods.
-NTU
methods.
Background
A heat exchanger is a device in which energy is transferred from one fluid to another across a solid surface. Exchanger analysis and design therefore involve both convection and conduction. Radiative transfer between the exchanger and the environment can usually be neglected unless the exchanger is uninsulated and its external surfaces are very hot.
Two important problems in heat exchanger analysis are (1) rating existing
heat exchangers and (ii) sizing heat exchangers for a particular application.
Rating involves determination of the rate of heat transfer, the change
in temperature of the two fluids, and the pressure drop across the heat
exchanger. Sizing involves selection of a specific heat exchanger from
those currently available or determining the dimensions for the design
of a new heat exchanger, given the required rate of heat transfer and allowable
pressure drop. The LMTD method can be readily used when the inlet and outlet
temperatures of both the hot and cold fluids are known. When the outlet
temperatures are not known, the LMTD can only be used in an iterative scheme.
In this case the  -NTU method can be used to
simplify the analysis.
-NTU method can be used to
simplify the analysis.
Energy Considerations
The first Law of Thermodynamics, in rate form, applied to a control volume (CV), can be expressed as
 (1)
(1)where 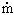 stands for mass-flow rate (e.g., 1bm/min
or kg/min) crossing the CV boundaries, h is specific enthalpy (energy/mass),
stands for mass-flow rate (e.g., 1bm/min
or kg/min) crossing the CV boundaries, h is specific enthalpy (energy/mass),  surris the rate of heat transfer from the CV to its surroundings,
and
surris the rate of heat transfer from the CV to its surroundings,
and  st is the rate of change of energy
stored in the CV. This simplified form of the First Law assumes no work-
producing processes, no energy generation inside the CV, and negligible
kinetic and potential energy in the fluid streams entering and leaving
the CV. In steady state operation the energy residing in the CV is constant,
meaning that
st is the rate of change of energy
stored in the CV. This simplified form of the First Law assumes no work-
producing processes, no energy generation inside the CV, and negligible
kinetic and potential energy in the fluid streams entering and leaving
the CV. In steady state operation the energy residing in the CV is constant,
meaning that  st=0. If, furthermore,
the boundary of the CV is adiabatic (i.e., perfectly insulated), then
st=0. If, furthermore,
the boundary of the CV is adiabatic (i.e., perfectly insulated), then  surr
=0. Under these circumstances Eq. (1) reduces to a simple balance
of enthalpy inflow and enthalpy outflow: .
surr
=0. Under these circumstances Eq. (1) reduces to a simple balance
of enthalpy inflow and enthalpy outflow: .
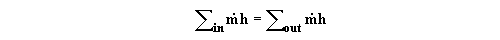 (2)
(2)Applied to a heat exchanger with two streams passing through it, Eq. (2) can be rearranged to give
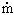 c(hc,o-hc,i) c(hc,o-hc,i)
| (3) |
where the subscripts h and c indicate the hot and cold fluids, respectively, and i and o indicate inlet and outlet conditions. In words, Eq. (3) says that the rate of energy loss by the hot fluid (left-hand side) equals the rate of energy gain by the cold fluid. Remember: This rate balance holds only if the heat-exchanger envelope is adiabatic and the exchanger has reached a steady state.
Shell and Tube Heat Exchanger
Figure 1 is a schematic diagram of a shell-and-tube heat exchanger
with one shell pass and one tube pass. The cross-counterflow mode of operation
is indicated.

Figure 1. Shell-and-tube-heat exchanger with one shell pass and one tube pass; cross- counterflow operation.
Inside the heat exchanger the hot and cold fluid temperature distributions would have the form sketched in Fig. 2(a).


The points 1 and 2 on the x axis represent the two ends of the heat
exchanger. Provided there is no energy loss to the environment and that
the exchanger has reached steady state, then dq, the rate of heat transfer
from the hot fluid, is exactly equal to the rate of heat transfer to the
cold fluid in a differential length dx of the exchanger surface. For the
special case of fluids that are not changing phase and have constant specific
heats
dq = - | (4) |
dq = | (5) |
q = Ch(Th,i-Th,o) | (6) |
q = Cc(Tc,o - Tc,i) | (7) |
The differential heat-transfer rate dq across the surface area element
dA can also be expressed as
dq = U | (8) |
where is the local temperature difference between the hot and cold fluids
and U is the overall coefficient of heat transfer at dA. Both U and T
vary with position inside the heat exchanger (i.e., x), but by combining
Eqs (4) and (5) with Eq. (8) it is possible for a single pass exchanger
to integrate over the exchanger contact surface from inlet to out. The
result of the integration is
T
vary with position inside the heat exchanger (i.e., x), but by combining
Eqs (4) and (5) with Eq. (8) it is possible for a single pass exchanger
to integrate over the exchanger contact surface from inlet to out. The
result of the integration is
q = AUm | (9) |
where q is the total heat-transfer rate (BTU/min), A is the total internal contact area (ft2), Um is the mean overall coefficient of heat transfer (BTU/min ft2º F), defined as
 (10)
(10) (11)
(11) T1 = T h,i-Tc,o
and
T1 = T h,i-Tc,o
and  T2 = Th,o-T c,i
for the counterflow, single pass case. Equation (9) is also applied to
more complicated heat-exchanger designs with multipass and cross- flow
arrangements with a correction factor applied to the LMTD. See Ozisik (1).
As mentioned above, if both inlet and outlet temperatures are specified
the LMTD can be calculated from Eq. (11) and q from either Eq. (6) or Eq.
(7). Then the product is given explicitly by Eq. (9). Further specification
of then "sizes" the heat exchanger, i.e., determines A and the dimensions
of the internal flow passages.
T2 = Th,o-T c,i
for the counterflow, single pass case. Equation (9) is also applied to
more complicated heat-exchanger designs with multipass and cross- flow
arrangements with a correction factor applied to the LMTD. See Ozisik (1).
As mentioned above, if both inlet and outlet temperatures are specified
the LMTD can be calculated from Eq. (11) and q from either Eq. (6) or Eq.
(7). Then the product is given explicitly by Eq. (9). Further specification
of then "sizes" the heat exchanger, i.e., determines A and the dimensions
of the internal flow passages.
2.  -NTU Method
-NTU Method
In cases where only the inlet temperatures of the hot and cold fluids
are known, the LMTD cannot be calculated beforehand and application of
the LMTD method requires an iterative approach. The recommended approach
is the effectiveness or  -NTU method. The heat-exchanger
effectiveness,
-NTU method. The heat-exchanger
effectiveness,  , is defined by
, is defined by
| (12) |
where q is the actual rate of heat transfer from the hot to cold fluid,
and qmax represents the maximum possible rate of heat transfer,
which is given by the relation
qmax = Cmin(Th,i- Tc,i) | (13) |
where Cmin is the smaller of the two heat capacity rates
(see above, Eqs (4) and (5). Thus, the actual heat transfer rate can be
expressed as
q = | (13) |
and calculated, given the heat-exchanger effectiveness  ,
the mass-flow rates and specific heats of the two fluids and the inlet
temperatures.
,
the mass-flow rates and specific heats of the two fluids and the inlet
temperatures.
The value of  depends on the heat-exchanger geometry and flow pattern (parallel flow,
counterflow, cross flow, etc.). Theoretical relations for
depends on the heat-exchanger geometry and flow pattern (parallel flow,
counterflow, cross flow, etc.). Theoretical relations for  and graphical characteristics are given by Ozisik (1) and Incropera &
DeWitt (2) for a limited selection of heat-exchanger types. For a single
pass counterflow exchanger like the one used in this exercise
and graphical characteristics are given by Ozisik (1) and Incropera &
DeWitt (2) for a limited selection of heat-exchanger types. For a single
pass counterflow exchanger like the one used in this exercise
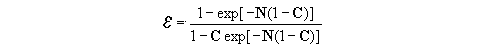 (15)
(15)where C Cmin / Cmax and
N
Cmin / Cmax and
N UmA / Cmin. The dimensionless
factor is known as the number of transfer units . It is an indicator of
the actual heat-transfer area or physical size of the exchanger. An experimental
determination of effectiveness is found by
UmA / Cmin. The dimensionless
factor is known as the number of transfer units . It is an indicator of
the actual heat-transfer area or physical size of the exchanger. An experimental
determination of effectiveness is found by
 (16)
(16)Apparatus
Figure A1 in the Appendix is a schematic diagram of the two flow loops
which exchange energy through the heat exchanger. Hot water circulates
through the exchanger shell while a chilled solution of propylene glycol
(PG) in water (approximately 30% PG by weight) circulates through the tubes.
The chilled water flow is driven by a constant speed centrifugal pump while
the hot water flow comes from the building water supply. Both flows are
controlled manually with valves. Mass flow rates are indicated by in-line
rotameter-type flow meters. Calibration curves for the two flow meters
are appended. Four thermocouples mounted close to the four ports of the
heat exchanger and connected to a digital readout indicate T h,i,Th,o
,Tc,i , and Tc,o.
The principal geometrical characteristics of the heat exchanger are
as follows:
Shell diameter (outer) 3.63 in. Shell length 27-1/4 in. Tube O.D. 0.250 in. Shell volume 0.70 gal. Tube volume(internal) 0.40 gal. Tube surface area 11.1 ft2 No. of tubes 76 Length of tubes 26-11/16 in.
Procedure
1. Locate the calibration data plot and equation for the water flow
meter in the lab write up.
2. Locate the calibration data plot and equation for the propylene glycol flow meter. Since this calibration was performed using water as the working fluid you must correct the equation for use with propylene glycol using the following relationship:
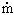 pg=
pg=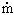 H2
O(S.G.pg)1/2
H2
O(S.G.pg)1/2The specific gravity (S.G.) of the propylene glycol is found on the graphics provided in the write- up for a 30% solution
3. Determine the flow meter readings for the sixteen experiments possible in the following array, choosing the water flow as the "minimum" fluid:
| C | (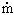 Cp)max [Btu/min°F] Cp)max [Btu/min°F]
| |||
|---|---|---|---|---|
| 1.00 | 5 | 10 | 20 | 40 |
| 0.75 | 5 | 10 | 30 | 60 |
| 0.50 | 7 | 15 | 30 | 60 |
| 0.25 | 15 | 30 | 45 | 65 |
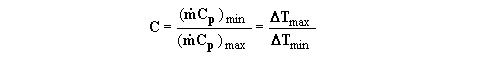 (17)
(17)From the first row (5, 10, 20, 40) you can determine the water flow meter readings as well as the propylene glycol flow meter readings, i.e., C = 1.0. From the "C" ratio, determine the other propylene glycol flow meter readings for the sixteen experiments using the values of Cp from the graph provided in the write-up.
4. Execution of the experiment
a) Set the H2O flow meter at the lowest reading in the array
and then monitor the difference between the inlet and outlet temperatures
for both water and propylene glycol (C = 1.0) until a steady state is established
(usually in a few minutes).
b) Measure and record the inlet, outlet and temperature difference for both the water and propylene glycol flows.
c) Change the propylene glycol flow to give C = .75, then .5 and .25, each time repeating a) and b) above.
d) Sequence through the second, third and fourth columns of the experimental
array.
5. Lab report.
a) Organize your lab data and calculated values in a neat spreadsheet
array. Use only the English system of units.
b) Plot the heat transfer to the propylene glycol vs. the log-mean-temperature difference.
c) From the sixteen experiments performed, determine the average overall heat transfer coefficient, U, from the following definition:
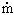 Cp)PG
Cp)PG TPG
= U A
TPG
= U A  TLMTD
TLMTDd) On one plot, plot the effectiveness,  ,
versus NTU and curve fit the data where C is a constant by making a plot
similar to Fig. 11.15 of Incropera & DeWitt using eq. (15). Remember
,
versus NTU and curve fit the data where C is a constant by making a plot
similar to Fig. 11.15 of Incropera & DeWitt using eq. (15). Remember  from your data is determined from the four measured temperatures using
eq. (16) and not from equation (15).
from your data is determined from the four measured temperatures using
eq. (16) and not from equation (15).

Appendix (Print out before coming to lab):
| Fig A1: | Schematic diagram, flow loops | |
| Fig A2: | Calibration curve for PENWALT flowmeter No. YYN-3447 | |
| Fig A3: | Calibration curve for Fischer & Porter flowmeter No. M2-1014/55 | |
| Fig A4: | Specific gravities of aqueous propylene glycol solutions. | |
| Fig A5: | Specific heats of aqueous propylene glycol solutions. |