Trilateration in Robotic Sensing Study Notes FL2010 Trilateration(what is)

<sidebar>Trilateration_in_Robotic_Sensing_using_Acoustic_Sensors_Nav</sidebar>

Trilateration

Trilateration is the procedure by which one can calculate the position of a target given the positions of other objects and the distances from the objects to the target. This process involves finding the intersection of spheres around the objects with radii equal to the distance to the target. The target will lie in the intersection. Commonly known forms of trilateration are global positioning systems (GPS). Each satellite knows where it is and how far it is from a receiver on Earth’s surface, Based on that information, the position of the receiver can be calculated.

The target to be located lies directly on the intersection of the circles. In order to make this calculation in 2D space, we need three of the red points. For instance, if we only had two of the red points, there would be two intersections, A and A’, and we would need another constraint to solve for the position, such as the target is above or below the dotted line.

However, in real life circumstances, there will be error in the estimation of the ranges, so we cannot just algebraically solve for the position. We need to estimate it some other way.

The following solution is a linearization of a system of equations, called the Linear Least Squares, derived by adding a subtracting the first constraint (x_1, y_1). This produces a matrix equation that will solve for the target position based on the estimated ranges and the positions of the anchor nodes.

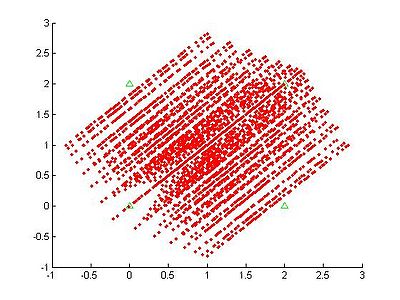
As mentioned in the range estimate section, there is certain resolution with which we can view the range from the target to an anchor node. If we assume this, applying that to the trilateration equations yields the following web (that is, points we can estimate the target to be given the locations of the anchor nodes).

The frequency used in this web is 1kHz, which is much less than the 50kHz used in our experiments. If we raise the frequency by much (more than another kHz) the web becomes too dense to see any changes in resolution. In other words, we have a very good resolution in our system.

An interesting thing to note is that linearization has done just that, linearized the possible solutions. In the figure, the first constraint was the node at 0,0, to the answers are lined up according to that node. If the first constraint were changed to be another node, the web would just rotate to be lineraized to that node.