Trilateration in Robotic Sensing using Acoustic Sensors Errors

<sidebar>Trilateration_in_Robotic_Sensing_using_Acoustic_Sensors_Nav</sidebar>

Error

Reducing error in our algorithm is one of the primary goals of this project. Accountable error can be attributed to two causes; quantization and noise.

Quantization

When our microphone hears the chirps it takes discrete samples. When we're estimating range, then, we can only place the source of each chirp at set intervals. More than likely the point we want to locate is not at one of those intervals but our algorithm will say it is. We are left with a quantization error which might be as large as half the distance between samples.

The following image illustrates this problem. The red lines represent the possible distances cross-correlation can report to us. Anything which falls between those lines has to be rounded to the nearest one. The green X, for instance, is a position we cannot calculate, and if our speaker were there we would have to say it was positioned either at the red line to the left or the one to the right, creating an error.

Reducing this Error: Increasing the sample rate reduces the space between these intervals, increasing or resolution and decreasing quantization error.

Noise

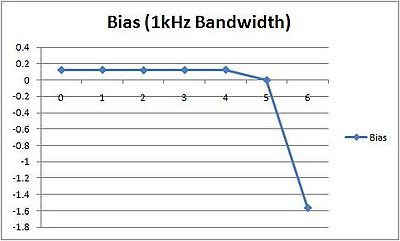
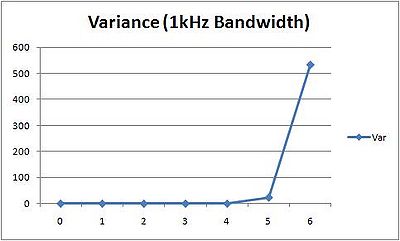
While our filters help isolate each signal, there will still be noise at any given frequency. Depending on how loud that noise is compared to the chirp, it can impact the results of cross-correlation and create an error. We ran a series of simulations to determine how large this effect was.

The simulations were conducted with a noise that had one fifth the amplitutde of the chirps and a standard deviation of 1. These parameters will vary from setup to setup. A chirp was created and suffered exponential decay over a specified distance, the noise was added, and cross-correlation was performed against the original chirp. We then compared the distance calculated by our algorithm to the distance specified at the outset of the simulation. At each meter distance we ran the simulation 5000 times and calculated the mean error or bias (meters) and the variance (meters squared). Plotted below:

There is a consistent bias having to do with quantization but for distances below a certain threshold (5 meters in this case) noise does not have a significant impact, as evidenced by the zero variance. Once the noise becomes similiar in volume to the chirp it takes over and results are chaotic. When noise is causing and error, you'll be able to see it.

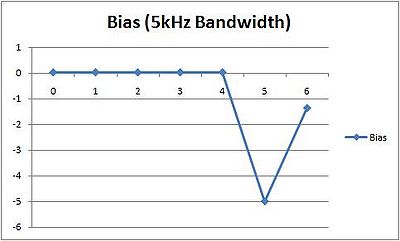
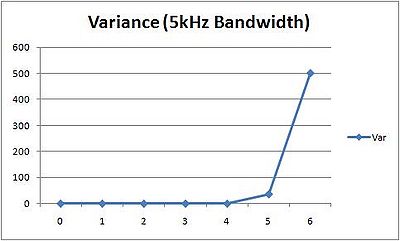
We repeated the above experiment with a chirp of 5kHz bandwidth (instead of 1kHz). The bias was much smaller and this demonstrates the effect of bandwidth on the quantization error. The results pertaining to noise were similiar. It has no effect close to the sound source but as the chirp's volume decays to comparable volumes, the noise creates a significant and alerting error.

Reducing this Error: ...