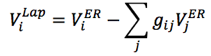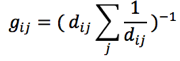Difference between revisions of "BCI-KurtusKahleFL2011"
Kurtus.kahle (talk | contribs) (Undo revision 2200 by Kurtus.kahle (Talk)) |
Kurtus.kahle (talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Abstract == | == Abstract == | ||
| − | This research project seeks to improve the signal quality of Brain-Computer Interfaces (BCIs) using existing and novel methods of spatial filtering. In this context, a spatial filter is any specified linear combination of signals from an electroencephalogram (EEG), and a BCI is any external device controlled by brain signals. Improved spatial filtering methods would result in better control of medical devices used to drive hand motion for stroke and traumatic brain injury patients, and may also aid such patients who require other forms of BCI (e.g. wheelchairs and communication devices). This project focuses on signals obtained from a specific model of EEG headset, the Emotiv EPOC, and on BCIs used to control an orthotic, robotic hand; however, these methods are applicable to other EEG configurations and other types of BCI. Existing spatial filtering methods include referencing one electrode to one other electrode (Bipolar), referencing to an average of all electrodes (Common Average Reference, or CAR), and an approximate spatial second derivative (Laplacian) reference. The novel method investigated herein uses an optimization routine to deduce spatial filters that outperform the standard methods on the | + | This research project seeks to improve the signal quality of Brain-Computer Interfaces (BCIs) using existing and novel methods of spatial filtering. In this context, a spatial filter is any specified linear combination of signals from an electroencephalogram (EEG), and a BCI is any external device controlled by brain signals. Improved spatial filtering methods would result in better control of medical devices used to drive hand motion for stroke and traumatic brain injury patients, and may also aid such patients who require other forms of BCI (e.g. wheelchairs and communication devices). This project focuses on signals obtained from a specific model of EEG headset, the Emotiv EPOC, and on BCIs used to control an orthotic, robotic hand; however, these methods are applicable to other EEG configurations and other types of BCI. Existing spatial filtering methods include referencing one electrode to one other electrode (Bipolar), referencing to an average of all electrodes (Common Average Reference, or CAR), and an approximate spatial second derivative (Laplacian) reference. The novel method investigated herein uses an optimization routine to deduce spatial filters that outperform the standard methods on the R^2 metric for a given signal – although the method could be used with other metrics, such as Receiver Operating Characteristic (ROC). The deduced filter is then applied to other data sets, and the new R^2 value is computed and compared to the R^2 values achieved using Bipolar, CAR, and Laplacian spatial filters, as well as the R^2 value obtained without a filter. Initial research indicates that none of the above spatial filters improve signal quality. These studies, however, may show promise in the future for stroke or traumatic brain injury patients who have difficulty with hand movement or several other basic tasks. |
== Background == | == Background == | ||
| Line 13: | Line 13: | ||
This research project uses an Emotiv EPOC EEG headset, but the methods presented herein are applicable to other electrode schemes. We selected this headset because EEG involves no significant risks and because the EPOC can be situated on the head in a few minutes rather than perhaps a half hour for some other EEG configurations. The EPOC has a total of 14 electrodes (Figure 1), so the spatial resolution of the data is much lower than for large-array (many electrodes) EEG systems. | This research project uses an Emotiv EPOC EEG headset, but the methods presented herein are applicable to other electrode schemes. We selected this headset because EEG involves no significant risks and because the EPOC can be situated on the head in a few minutes rather than perhaps a half hour for some other EEG configurations. The EPOC has a total of 14 electrodes (Figure 1), so the spatial resolution of the data is much lower than for large-array (many electrodes) EEG systems. | ||
| − | After acquired, the signal is Fast Fourier Transformed into the frequency domain. Hence, we have power spectra for each electrode, for a variety of frequency bins, and for a few test conditions of our choosing. At this point, we can directly compute the | + | [[File:fig1.png]] |
| + | |||
| + | After acquired, the signal is Fast Fourier Transformed into the frequency domain. Hence, we have power spectra for each electrode, for a variety of frequency bins, and for a few test conditions of our choosing. At this point, we can directly compute the R^2 statistic for each electrode and frequency bin, comparing two trial conditions. In this experiment, we compare hand motions to the hand at rest to compute the statistic. R^2 is a unitless measurement of how reliably the signals differ for the two trial conditions, i.e. how consistent and different the signals are for those conditions. It ranges from 0 (not reliable) to 1 (perfectly reliable). For example, if moving the right hand consistently produces a power reduction in the 12-Hz bin for the F7 electrode (figure 2), that bin and electrode will have a high R^2 (close to 1). If there is no consistent difference between the two trial conditions and the spectrum does not seem to depend on the trial condition, R^2 will be low (close to 0). With this headset and signal processing method, a somewhat trained subject might show R^2 values from about 0.3 to 0.5 at a few frequency bins, on a few electrodes. This result means that 30% to 50% of the variance between signals from different test conditions (for a given bin and electrode) can be accounted for by the change in test condition. Since we would like the result to approach 1, we wish to apply new and existing methods to improve signal quality and reduce noise. | ||
| + | |||
| + | [[File:fig2.png]] | ||
== Spatial Filtering == | == Spatial Filtering == | ||
| Line 19: | Line 23: | ||
Up to now, a few different schemes of spatial filtering have been used. When acquiring a signal, each electrode is generally referenced to another electrode behind the ear, which is referred to as “ear reference.” Figure 3 shows some common spatial filters in the context of large-array EEG systems. Common average reference (CAR) refers to a filter for which the average of the signals from every electrode is taken as the zero. A bipolar filter is the simple subtraction of one electrode’s signal from another. A Laplacian filter attempts to approximate a signal's spatial second derivative. For a small Laplacian filter, an average, weighted by distance, of the four nearest neighbor electrodes is computed and used as the reference. For a large Laplacian filter, the next-nearest neighbors are used in place of the nearest neighbors [7]. | Up to now, a few different schemes of spatial filtering have been used. When acquiring a signal, each electrode is generally referenced to another electrode behind the ear, which is referred to as “ear reference.” Figure 3 shows some common spatial filters in the context of large-array EEG systems. Common average reference (CAR) refers to a filter for which the average of the signals from every electrode is taken as the zero. A bipolar filter is the simple subtraction of one electrode’s signal from another. A Laplacian filter attempts to approximate a signal's spatial second derivative. For a small Laplacian filter, an average, weighted by distance, of the four nearest neighbor electrodes is computed and used as the reference. For a large Laplacian filter, the next-nearest neighbors are used in place of the nearest neighbors [7]. | ||
| + | |||
| + | [[File:fig3.png]] | ||
Both the small and large Laplacian filters are defined by the following equation: | Both the small and large Laplacian filters are defined by the following equation: | ||
| − | + |  | |
| + | |||
| + | [[File:eq1.png]] | ||
| + | |||
where | where | ||
| − | + | ||
| + | [[File:eq2.png]] | ||
| + | |||
and where V refers to voltages, Lap indicates Laplacian, ER indicates ear reference, and j indexes the nearest neighbor electrodes. | and where V refers to voltages, Lap indicates Laplacian, ER indicates ear reference, and j indexes the nearest neighbor electrodes. | ||
| Line 37: | Line 48: | ||
== Optimizing Spatial Filters == | == Optimizing Spatial Filters == | ||
| − | This project presents a novel method of determining spatial filters. Rather than using an invented scheme such as Bipolar, Laplacian, or CAR, this method uses an optimization routine to determine the filter. Starting with a set of signals and an initial filter, MATLAB's fminsearch function varies the spatial filter, attempting to maximize | + | This project presents a novel method of determining spatial filters. Rather than using an invented scheme such as Bipolar, Laplacian, or CAR, this method uses an optimization routine to determine the filter. Starting with a set of signals and an initial filter, MATLAB's fminsearch function varies the spatial filter, attempting to maximize R^2. Optimization methods may produce higher values of R^2 than other methods, but they are highly subject to over-training. In other words, the filter produced may work excellently on the data set used for training but poorly for other data sets. Additionally, this method also only produces local maxima. The output will be the best filter that resembles the initial filters and similar filters; however, there may very well exist a filter that achieves a higher R^2 for that data set, or more importantly, for any arbitrary data set produced by a given subject. |
== Temporal Alignment == | == Temporal Alignment == | ||
| Line 45: | Line 56: | ||
This study’s test subject was a healthy female, age 20. The EPOC observed the subject’s brain signals for three trial conditions: actively moving the left hand, actively moving the right hand, and rest. The subject was instructed to keep all hand motions consistent and not to blink during the trials, as eyeblinks create noise of several times greater amplitude than the rest of the signal. The subject participated for three 15-minute sessions, during which the trial condition varied at random between the three possibilities. The subject received no sensory feedback on the real-time signal quality. | This study’s test subject was a healthy female, age 20. The EPOC observed the subject’s brain signals for three trial conditions: actively moving the left hand, actively moving the right hand, and rest. The subject was instructed to keep all hand motions consistent and not to blink during the trials, as eyeblinks create noise of several times greater amplitude than the rest of the signal. The subject participated for three 15-minute sessions, during which the trial condition varied at random between the three possibilities. The subject received no sensory feedback on the real-time signal quality. | ||
| − | All data were analyzed off-line. First, | + | All data were analyzed off-line. First, R^2 was computed for ear reference filters, the CAR filter, all possible bipolar filters, and the aforementioned modified version of Laplacian filtering. Next, the first 80% of the data set from each of the three trials (the “training set”) was run through the optimization routine, each using three different initial spatial filters. The first initial filter was the zero vector. Since we expect the most useful signals to originate in the regions of the brain associated with planning and motor skills, the second initial filter had 1 as the weight for electrodes AF3 & 4; F3, 4, 7, & 8; and FC5 & 6, and a zero for all other electrodes. The third initial filter was estimated based on results from each data set. It was roughly CAR, but with select electrodes – those channels with high relative R^2 values for a given data set – weighted positively and more heavily. |
| − | + | R^2 values were computed for each training data set using all nine output filters. Each training set corresponds to a “testing set,” namely the other 20% of each of the initial data sets. For each initial data set, the three output filters were applied to the corresponding testing set and R^2 was computed. Finally, R^2 was computed for each complete data set using the third (estimated) filter. This process was completed for data sets before and after temporal alignment. | |
== Results and discussion == | == Results and discussion == | ||
| − | In general, ear reference spatial filters produced higher | + | In general, ear reference spatial filters produced higher R^2 values than Laplacian, bipolar, or common average reference filters. In the case of the data set corresponding to the third session, where ear reference filters produced a lower R^2 value (0.36 as opposed to .60 and .51, respectively), both bipolar and CAR somewhat outperformed ear reference filters. The significantly lower R^2 value in the third set indicates that some additional source of noise may have been more present in that trial than in the other trials likely eyeblinks. If this assumption is true, then the spatial filters may have been effective in reducing the effect of this noise. |
Seven out of nine optimized spatial filters performed better than ear reference or any other spatial filter when applied to the training set (i.e. the set used for the optimization routine), on average 5% better than ear reference. However, the optimized filters nearly all performed worse than ear reference filters on the testing sets, which indicates that the spatial filters were over-trained. These filters performed especially poorly on unrelated sets (i.e. the other two sets). | Seven out of nine optimized spatial filters performed better than ear reference or any other spatial filter when applied to the training set (i.e. the set used for the optimization routine), on average 5% better than ear reference. However, the optimized filters nearly all performed worse than ear reference filters on the testing sets, which indicates that the spatial filters were over-trained. These filters performed especially poorly on unrelated sets (i.e. the other two sets). | ||
| − | Temporal alignment only produced slightly different results with the previously existing spatial filtering methods. The output spatial filters and | + | Temporal alignment only produced slightly different results with the previously existing spatial filtering methods. The output spatial filters and R^2 values did differ when alignment was coupled with the optimization routine, but alignment did not consistently improve or worsen those results. |
| − | In general, the following spatial filters consistently (across sets) produced | + | In general, the following spatial filters consistently (across sets) produced R^2 values reasonably close to the maximum for that set: ear reference, Laplacian, bipolar, CAR, and optimized filters derived from estimated initial filters. The only filters that consistently performed very well across all sets were ear reference filters. |
== Conclusions and further research == | == Conclusions and further research == | ||
| Line 62: | Line 73: | ||
First, this study used only three data sets from a single subject. Substantially more sets should be acquired from several more subjects who vary in age, sex, and health1. Additionally, subjects must be trained considerably, to the point that they consistently produce similar results, which was not the case for this subject (figure 4). The same procedures may very well have produced better results if the subject were highly trained. | First, this study used only three data sets from a single subject. Substantially more sets should be acquired from several more subjects who vary in age, sex, and health1. Additionally, subjects must be trained considerably, to the point that they consistently produce similar results, which was not the case for this subject (figure 4). The same procedures may very well have produced better results if the subject were highly trained. | ||
| + | |||
| + | [[File:fig4a.png]] [[File:fig4b.png]] [[File:fig4c.png]] | ||
| + | |||
| + | [[File:fig4cap.png]] | ||
Second, eyeblinks can substantially impair results, and are commonly a major source of problems in BCI studies [9]. The subject was instructed not to blink during trials, but it is extremely difficult to avoid doing so. Future studies should control for eyeblinks either by detecting them and throwing out trials that contain too many eyeblinks, or by removing eyeblinks using signal processing techniques. | Second, eyeblinks can substantially impair results, and are commonly a major source of problems in BCI studies [9]. The subject was instructed not to blink during trials, but it is extremely difficult to avoid doing so. Future studies should control for eyeblinks either by detecting them and throwing out trials that contain too many eyeblinks, or by removing eyeblinks using signal processing techniques. | ||
| − | Third, | + | Third, R^2 was used as the sole metric for signal quality, but many other classifiers and metrics for signal quality exist. Future studies should attempt similar procedures using several different classifiers and metrics, such as receiver operating characteristic (ROC) and principal component analysis (PCA). |
| − | Fourth, this study used fminsearch with a certain set of parameters to optimize on | + | Fourth, this study used fminsearch with a certain set of parameters to optimize on R^2. Other sets of parameters and other optimization techniques exist, and they should be incorporated into future studies. |
| − | Finally, the estimated filter used as an initial point for the optimization routine performed surprisingly well on its own. Researchers should develop and test algorithms to estimate spatial filters based on the various | + | Finally, the estimated filter used as an initial point for the optimization routine performed surprisingly well on its own. Researchers should develop and test algorithms to estimate spatial filters based on the various R^2 values (or another metric) obtained from each electrode. |
Additionally, if and when this research begins to show promise for improving signal quality, the techniques presented herein and elsewhere could be used to develop multiple spatial filters for the same subject but different motions. Such differing spatial filters could produce independent triggers for a BCI, resulting in multidimensional control. | Additionally, if and when this research begins to show promise for improving signal quality, the techniques presented herein and elsewhere could be used to develop multiple spatial filters for the same subject but different motions. Such differing spatial filters could produce independent triggers for a BCI, resulting in multidimensional control. | ||
| + | |||
| + | == Addendum == | ||
| + | The following document by Elad Gilboa is available for more information about the R^2 statistic and F-test for BCI applications: | ||
| + | |||
| + | [[File:rsqu.pdf]] | ||
== References == | == References == | ||
Latest revision as of 06:47, 26 April 2012
Contents
Abstract
This research project seeks to improve the signal quality of Brain-Computer Interfaces (BCIs) using existing and novel methods of spatial filtering. In this context, a spatial filter is any specified linear combination of signals from an electroencephalogram (EEG), and a BCI is any external device controlled by brain signals. Improved spatial filtering methods would result in better control of medical devices used to drive hand motion for stroke and traumatic brain injury patients, and may also aid such patients who require other forms of BCI (e.g. wheelchairs and communication devices). This project focuses on signals obtained from a specific model of EEG headset, the Emotiv EPOC, and on BCIs used to control an orthotic, robotic hand; however, these methods are applicable to other EEG configurations and other types of BCI. Existing spatial filtering methods include referencing one electrode to one other electrode (Bipolar), referencing to an average of all electrodes (Common Average Reference, or CAR), and an approximate spatial second derivative (Laplacian) reference. The novel method investigated herein uses an optimization routine to deduce spatial filters that outperform the standard methods on the R^2 metric for a given signal – although the method could be used with other metrics, such as Receiver Operating Characteristic (ROC). The deduced filter is then applied to other data sets, and the new R^2 value is computed and compared to the R^2 values achieved using Bipolar, CAR, and Laplacian spatial filters, as well as the R^2 value obtained without a filter. Initial research indicates that none of the above spatial filters improve signal quality. These studies, however, may show promise in the future for stroke or traumatic brain injury patients who have difficulty with hand movement or several other basic tasks.
Background
Due to conditions such as stroke and traumatic brain injury, approximately 900,000 Americans have difficulty grasping objects with their hands [1]. Patients with these disorders often cannot complete otherwise simple actions such as holding a glass of water or hand-writing a note. The same disorders may also cause significant losses in speech and mobility. Often, the patients maintain the cognitive ability to communicate and move, but lack the neural pathways to complete these actions. Brain-Computer Interfaces (BCI’s) may offer a solution to this problem by establishing a secondary connection between the brain and the outside world, via computer [2].
Brain-Computer Interfaces
A Brain-Computer Interface is any external, manmade device controlled by brain signals. This research focuses on BCI's used to control hand motion, but it may be extended to other devices, such as wheelchairs and communication devices. Good candidates for any of these devices must have retained moderate or strong cognitive abilities. If patients possess the ability to think about the desired action (e.g. opening the left hand, moving the wheelchair forward, or communicating a specific word), they can produce the brain signals necessary to trigger a BCI. Initially, brain signals may not consistently and effectively trigger the BCI because thinking about the action may not automatically produce the type or quality of brain signals that the system readily recognizes. The brain, however, can learn to manipulate its waves at the certain frequencies (usually the mu or alpha rhythms, i.e. 8-12 Hz and 18-26 Hz, respectively) over time. Therefore, learning to use a BCI requires dozens of hours of practice, and candidate patients must be able to maintain focus for long periods of time [3].
Signal Acquisition and Processing
Signals are acquired from electrodes using either electroencephalography (EEG – electrodes on the scalp) or electrocorticography (ECoG – electrodes immediately below the surface of the skull). Since ECoG electrodes are located directly on the surface of the brain, they produce much higher signal quality and much less noise than EEG electrodes, which are separated from the brain by the scalp and skull. However, situating ECoG electrodes requires drilling through the skull, which carries risks and is not consistently approved by the FDA [4].
This research project uses an Emotiv EPOC EEG headset, but the methods presented herein are applicable to other electrode schemes. We selected this headset because EEG involves no significant risks and because the EPOC can be situated on the head in a few minutes rather than perhaps a half hour for some other EEG configurations. The EPOC has a total of 14 electrodes (Figure 1), so the spatial resolution of the data is much lower than for large-array (many electrodes) EEG systems.
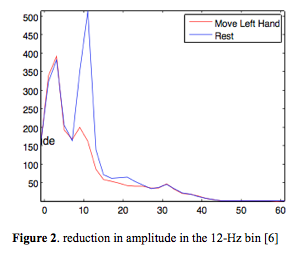
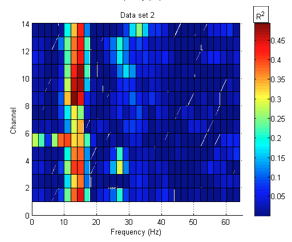
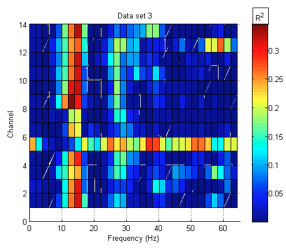
After acquired, the signal is Fast Fourier Transformed into the frequency domain. Hence, we have power spectra for each electrode, for a variety of frequency bins, and for a few test conditions of our choosing. At this point, we can directly compute the R^2 statistic for each electrode and frequency bin, comparing two trial conditions. In this experiment, we compare hand motions to the hand at rest to compute the statistic. R^2 is a unitless measurement of how reliably the signals differ for the two trial conditions, i.e. how consistent and different the signals are for those conditions. It ranges from 0 (not reliable) to 1 (perfectly reliable). For example, if moving the right hand consistently produces a power reduction in the 12-Hz bin for the F7 electrode (figure 2), that bin and electrode will have a high R^2 (close to 1). If there is no consistent difference between the two trial conditions and the spectrum does not seem to depend on the trial condition, R^2 will be low (close to 0). With this headset and signal processing method, a somewhat trained subject might show R^2 values from about 0.3 to 0.5 at a few frequency bins, on a few electrodes. This result means that 30% to 50% of the variance between signals from different test conditions (for a given bin and electrode) can be accounted for by the change in test condition. Since we would like the result to approach 1, we wish to apply new and existing methods to improve signal quality and reduce noise.
Spatial Filtering
Noise often appears in specific spatial patterns. For example, noise may be common to some area of the scalp and hence picked up by multiple electrodes. If the noise is common to two electrodes but the desired signal is only detected by one electrode, the difference between the respective signals will contain only the signal and not the noise. Hence, linear combinations of signals, known as “spatial filters,” may eliminate, or filter, noise by considering the spatial distributions of the noise with respect to the electrodes. For the commonly used spatial filters, a “zero,” taken as a weighted sum of signals of other electrodes, is subtracted from the signal of another electrode.
Up to now, a few different schemes of spatial filtering have been used. When acquiring a signal, each electrode is generally referenced to another electrode behind the ear, which is referred to as “ear reference.” Figure 3 shows some common spatial filters in the context of large-array EEG systems. Common average reference (CAR) refers to a filter for which the average of the signals from every electrode is taken as the zero. A bipolar filter is the simple subtraction of one electrode’s signal from another. A Laplacian filter attempts to approximate a signal's spatial second derivative. For a small Laplacian filter, an average, weighted by distance, of the four nearest neighbor electrodes is computed and used as the reference. For a large Laplacian filter, the next-nearest neighbors are used in place of the nearest neighbors [7].
Both the small and large Laplacian filters are defined by the following equation: 
where
and where V refers to voltages, Lap indicates Laplacian, ER indicates ear reference, and j indexes the nearest neighbor electrodes.
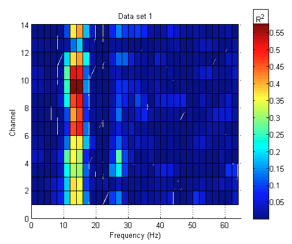
It is visually evident based on figures 2 and 3 that we cannot take the same approach for Laplacian filters on the EPOC as on standard EEG arrays. On standard clinical arrays, the electrodes are laid out in a grid; hence, the nearest neighbors can be selected as the electrodes immediately (for small laplacian) “North,” “South,” “East,” and “West” of the selected electrode. Since electrode do not consistently reside in the “cardinal directions” for the EPOC headset, we chose the following schemes for the left hand side:
electrode: references AF3: F7, F3 F7: AF3, FC5 F3: AF3, FC5, F4 FC5: F7, F3, T7
The rest of the left side remains ear reference because those areas of the head should not be related with motor control. We used the mirror image of the above schemes for the right hand side.
Optimizing Spatial Filters
This project presents a novel method of determining spatial filters. Rather than using an invented scheme such as Bipolar, Laplacian, or CAR, this method uses an optimization routine to determine the filter. Starting with a set of signals and an initial filter, MATLAB's fminsearch function varies the spatial filter, attempting to maximize R^2. Optimization methods may produce higher values of R^2 than other methods, but they are highly subject to over-training. In other words, the filter produced may work excellently on the data set used for training but poorly for other data sets. Additionally, this method also only produces local maxima. The output will be the best filter that resembles the initial filters and similar filters; however, there may very well exist a filter that achieves a higher R^2 for that data set, or more importantly, for any arbitrary data set produced by a given subject.
Temporal Alignment
Rather than sampling all electrodes simultaneously once every sampling period, most EEG and ECoG systems sample each electrode sequentially. This distinction is generally of no consequence for BCI's with simple spatial filtering schemes, but it can create significant noise in systems using electrodes sampled at substantially different times. This significant noise tends to occur when distant electrodes or many electrodes are combined [7]. Many EEG systems (e.g. [7]) sample at 128 Hz. If there are 64 electrodes, this could produce a phase difference between electrodes of about 8 ms. The Emotiv EPOC does output at 128 Hz, but it samples internally at 2048 Hz, so it will produce a maximum phase difference of about 0.5 ms [8].
Methods
This study’s test subject was a healthy female, age 20. The EPOC observed the subject’s brain signals for three trial conditions: actively moving the left hand, actively moving the right hand, and rest. The subject was instructed to keep all hand motions consistent and not to blink during the trials, as eyeblinks create noise of several times greater amplitude than the rest of the signal. The subject participated for three 15-minute sessions, during which the trial condition varied at random between the three possibilities. The subject received no sensory feedback on the real-time signal quality.
All data were analyzed off-line. First, R^2 was computed for ear reference filters, the CAR filter, all possible bipolar filters, and the aforementioned modified version of Laplacian filtering. Next, the first 80% of the data set from each of the three trials (the “training set”) was run through the optimization routine, each using three different initial spatial filters. The first initial filter was the zero vector. Since we expect the most useful signals to originate in the regions of the brain associated with planning and motor skills, the second initial filter had 1 as the weight for electrodes AF3 & 4; F3, 4, 7, & 8; and FC5 & 6, and a zero for all other electrodes. The third initial filter was estimated based on results from each data set. It was roughly CAR, but with select electrodes – those channels with high relative R^2 values for a given data set – weighted positively and more heavily.
R^2 values were computed for each training data set using all nine output filters. Each training set corresponds to a “testing set,” namely the other 20% of each of the initial data sets. For each initial data set, the three output filters were applied to the corresponding testing set and R^2 was computed. Finally, R^2 was computed for each complete data set using the third (estimated) filter. This process was completed for data sets before and after temporal alignment.
Results and discussion
In general, ear reference spatial filters produced higher R^2 values than Laplacian, bipolar, or common average reference filters. In the case of the data set corresponding to the third session, where ear reference filters produced a lower R^2 value (0.36 as opposed to .60 and .51, respectively), both bipolar and CAR somewhat outperformed ear reference filters. The significantly lower R^2 value in the third set indicates that some additional source of noise may have been more present in that trial than in the other trials likely eyeblinks. If this assumption is true, then the spatial filters may have been effective in reducing the effect of this noise.
Seven out of nine optimized spatial filters performed better than ear reference or any other spatial filter when applied to the training set (i.e. the set used for the optimization routine), on average 5% better than ear reference. However, the optimized filters nearly all performed worse than ear reference filters on the testing sets, which indicates that the spatial filters were over-trained. These filters performed especially poorly on unrelated sets (i.e. the other two sets).
Temporal alignment only produced slightly different results with the previously existing spatial filtering methods. The output spatial filters and R^2 values did differ when alignment was coupled with the optimization routine, but alignment did not consistently improve or worsen those results.
In general, the following spatial filters consistently (across sets) produced R^2 values reasonably close to the maximum for that set: ear reference, Laplacian, bipolar, CAR, and optimized filters derived from estimated initial filters. The only filters that consistently performed very well across all sets were ear reference filters.
Conclusions and further research
Although the research presented herein may not yet confirm that spatial filters can significantly and consistently improve signal quality of EEG signals for BCI applications, that result has certainly been shown in the past [7]. Several confounding factors influenced the results of this study, many of which could be improved in continuing research and subsequent studies. Several of those factors are listed here:
First, this study used only three data sets from a single subject. Substantially more sets should be acquired from several more subjects who vary in age, sex, and health1. Additionally, subjects must be trained considerably, to the point that they consistently produce similar results, which was not the case for this subject (figure 4). The same procedures may very well have produced better results if the subject were highly trained.
Second, eyeblinks can substantially impair results, and are commonly a major source of problems in BCI studies [9]. The subject was instructed not to blink during trials, but it is extremely difficult to avoid doing so. Future studies should control for eyeblinks either by detecting them and throwing out trials that contain too many eyeblinks, or by removing eyeblinks using signal processing techniques.
Third, R^2 was used as the sole metric for signal quality, but many other classifiers and metrics for signal quality exist. Future studies should attempt similar procedures using several different classifiers and metrics, such as receiver operating characteristic (ROC) and principal component analysis (PCA).
Fourth, this study used fminsearch with a certain set of parameters to optimize on R^2. Other sets of parameters and other optimization techniques exist, and they should be incorporated into future studies.
Finally, the estimated filter used as an initial point for the optimization routine performed surprisingly well on its own. Researchers should develop and test algorithms to estimate spatial filters based on the various R^2 values (or another metric) obtained from each electrode.
Additionally, if and when this research begins to show promise for improving signal quality, the techniques presented herein and elsewhere could be used to develop multiple spatial filters for the same subject but different motions. Such differing spatial filters could produce independent triggers for a BCI, resulting in multidimensional control.
Addendum
The following document by Elad Gilboa is available for more information about the R^2 statistic and F-test for BCI applications:
References
[1] US Census Bureau. (2005) Prevalence of Disability Among Individuals 15 Years and Older by Specific Measures of Disability. [Online]. http://www.census.gov/hhes/www/disability/sipp/disab05/d05tb1.pdf
[2] Eric C. Leuthardt, Gerwin Schalk, Daniel Moran, Jeffrey G. Ojemann, “The Emerging World of Motor Neuroprosthetics: A Neurosurgical Perspective,” Neurosurgery, vol. 58, pp. 1-14, 2006.
[3] Jonathan R .Wolpaw and Dennis J. McFarland, "Control of a two-dimensional movement signal by a noninvasive brain-computer interface in humans," Proc. Natl. Acad. Sci, vol. 101,no. 51, pp. 17849-17854, December 2004.
[4] Jonathan Wolpaw, Elizabeth Winter Wolpaw, Brain-Computer Interfaces. New York: Oxford University Press, 2012.
[5] André Hoffmann, “EEG Signal Processing and Emotiv’s Neuro Headset,” Bachelor’s Thesis, Technische Universität Darmstadt.
[6] Courtesy of Samuel Fok, Washington University.
[7] Dennis J. McFarland, Lynn M. McCane, Stephen V. David, Jonathan R. Wolpaw, “Spatial filter selection for EEG-based communication,” Electroencephalography and clinical Neurophysiology, vol. 103, pp. 386-394, 1997.
[8] Geoff Mackellar, personal communication.
[9] Johnathan R. Wolpaw, Niels Birbaumer, Dennis J. McFarland, Gert Pfurtscheller, Theresa M. Vaughan.