
Scheme of the domain for Benard-Marangoni instability
Principle
of Benard-Marangoni instability
Manifestations
of Benard-Marangoni instability
Principle of Benard-Marangoni instability
This instability studied by Benard in the beginning of the XXth century is sometimes abashed with Rayleigh-Benard instability.
Benard-Marangoni instability is a free surface configuration of Rayleigh-Benard instability. In fact, a thin layer of fluid is placed on a horizontal plane but its upper face is not in contact with an other plane but it is a free surface in contact with the air. The temperature of the lower plane must be superior to the temperature of the air to develop instabilities.

Scheme of the domain for Benard-Marangoni instability
This instability appear thanks to a gradient of surface
tension at the free surface due to a temperature perturbation. If for example,
local temperature on the free surface is superior from equilibrum temperature,
there is a gradient of surface tension which ejects radialy the fluid from the
heated region to exterior where temperature is more cold. To preserv mass, hot
fluid ascends from the lower plane. So there is a system of cells which sets up
and inside cells fluid goes up by the center of cells and goes down by the
periphery of cells.
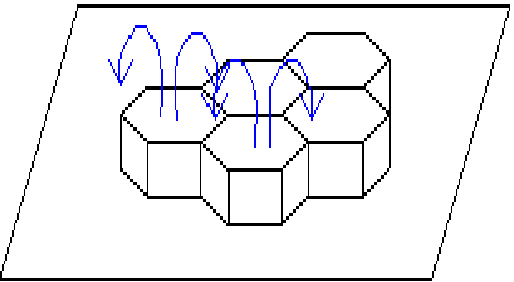
Scheme of hexagonal cells of Benard-Marangoni
 |
 |
In this case, the adimensional parameter which determines the threshold is the Marangoni number :
![]()
The critical value of Marangoni number to develop instabilities is :
![]()
Manifestation of Benard-Marangoni
instability
This instability looks like Rayleigh-Benard instability. So manifestations of it are the same than manifestations of Rayleigh-Benard instability. For this reason we are not going to explain here manifestations of Benard-Marangoni instability (See Manifestations of Rayleigh-Benard instability).