6.6.1 Sliding constraint

Products: ABAQUS/Standard ABAQUS/Explicit
The sliding constraint has a variety of uses. For example, this MPC is used in conjunction with other MPC types to constrain a shell element mesh to a solid element mesh. The MPC maintains consistency with standard shell theory by forcing initially straight lines through the thickness to remain straight despite rotation and displacement. When applied to solid element nodes on the shell-solid interface, this MPC enforces a kinematic approximation of compatibility with the shell model.
The theory of this constraint is as follows:
Let 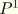 ,
, 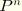 be the points defining the line; and let
be the points defining the line; and let 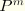 be the node that must lie on this line. The direction of the line is given by
be the node that must lie on this line. The direction of the line is given by
where
Let
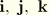
be base vectors in the
x-,
y-,
z-directions in the global coordinate system. Then, define a unit vector normal to the line as
unless
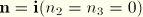
, in which case we use
Now we can define an orthogonal normal as
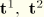
, and
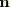
now form a set of orthonormal base vectors with
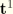
and
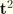
normal to the line joining
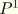
and
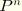
. The constraint can be imposed by the condition that the line joining the node
m to node 1 be perpendicular to
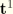
and
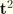
; that is,
and
We now choose a local coordinate numbering system such that
i is the global direction on which
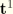
has its largest projection:
Likewise, we choose global direction
j such that
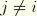
and
Using this definition of
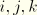
the constraint conditions can be written explicitly in terms of coordinate components of node
m as
and
These equations can be used to eliminate
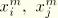
(note that the numbering of
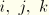
avoids dividing through by zero in this elimination):
and
The above equations will enforce the desired constraint. We also need the derivatives of these constraints. These are
and
where
and
These equations reduce to
and
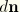
can be obtained from the definition of
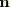
to give
and, therefore,
and
The incremental constraint equations become
and
Let
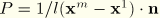
. Then, the above equations, when written out in full with the same ordering of
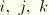
used above, are
and
Solving for
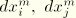
we obtain
and
In the two-dimensional case 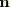 lies in the x–y or r–z plane and
lies in the x–y or r–z plane and 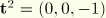 . This implies that the second constraint equation is satisfied automatically. The remaining constraint equation is
. This implies that the second constraint equation is satisfied automatically. The remaining constraint equation is
and its derivative is

![]() ,
, ![]() be the points defining the line; and let
be the points defining the line; and let ![]() be the node that must lie on this line. The direction of the line is given by
be the node that must lie on this line. The direction of the line is given by ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
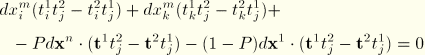
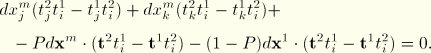
![]() lies in the x–y or r–z plane and
lies in the x–y or r–z plane and ![]() . This implies that the second constraint equation is satisfied automatically. The remaining constraint equation is
. This implies that the second constraint equation is satisfied automatically. The remaining constraint equation is ![]()
![]()