Products: ABAQUS/Standard ABAQUS/Explicit
The metal plasticity models in ABAQUS use the Mises stress potential for isotropic behavior and the Hill stress potentials for anisotropic behavior. Both of these potentials depend only on the deviatoric stress, so the plastic part of the response is incompressible. This means that, in cases where the plastic flow dominates the response (such as limit load calculations or metal forming problems), except for plane stress problems, the finite elements should be chosen so that they can accommodate the incompressible flow. Usually the reduced integration elements are used for this purpose: in ABAQUS/Standard the “hybrid” elements can also be used, at higher cost. The fully integrated first-order continuum elements in ABAQUS/Standard use selectively reduced integration, whereby the volumetric strain is calculated at the centroid of the element only. Those elements that are described in “Solid isoparametric quadrilaterals and hexahedra,” Section 3.2.4, are also suitable for such problems.
The Mises stress potential is
![]()
![]()
![]()
The potential is a circle in the plane normal to the hydrostatic axis in principal stress space. For this function,
![]()
![]()
Hill's stress function is a simple extension of the Mises function to allow anisotropic behavior. The function is
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For this function
![]()
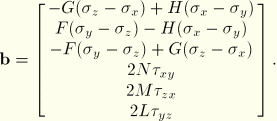
In addition,
![]()