The MASS and ROTARYI elements allow the inertia of a rigid body to be introduced at a node. In this section the formulation used with these elements is defined.

It is assumed that the node at which the mass and rotary inertia are introduced is the center of mass of the body. We refer to the node as the rigid body reference node, C. Let the local principal axes of inertia of the body be 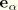, 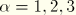. Let be the vector between C and some point in the rigid body with current coordinates , so that

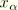
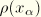
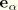
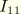
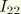
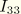
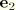
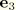
where are local coordinates in the rigid body. The mass of the rigid body is the integral of the mass density over the body Since C is assumed to be the center of mass of the body, Since the are the principal axes of the body, Let , , and be the second moments of inertia of the body about its principal axes , , and ; then The rotary inertia tensor is written

For a rigid body the velocity of any point in the body is given by

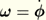
where is the angular velocity of the body. Taking a second time derivative, the acceleration is

The local or strong form of the equilibrium equations represents the balance of linear momentum and balance of angular momentum; these two equilibrium equations are

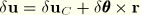
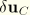
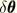
The variational or weak form of equilibrium is The internal or d'Alembert force contribution is where is the variation of the position of a point in the body. Here is the variation of the position of the rigid body reference node, and is the variation of the rotation of the rigid body reference node. The external loading contribution is Introducing component expressions relative to the principal axes of inertia, the rotational contribution to the weak form becomes

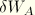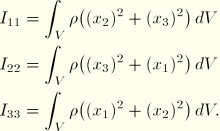
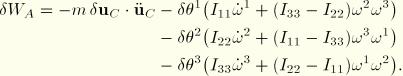
When the inertia of a rigid body is used with implicit time integration, the Jacobian contribution of is required: this is