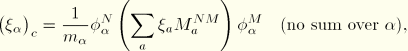The “generalized mass” associated with mode is

where is the structure's mass matrix and is the eigenvector for mode . The superscripts N and M refer to degrees of freedom of the finite element model.

ABAQUS/Standard allows the user to choose between two types of eigenvector normalization: the eigenvectors can be scaled so that the largest entry in each vector is unity, or they can be normalized so that the generalized mass for each vector is unity (). The choice of eigenvector normalization type does not influence the results of subsequent modal dynamic steps. The normalization type determines only the manner in which the eigenvectors are represented.

The participation factor for mode in direction i, , is a variable that indicates how strongly motion in the global x-, y- or z-direction or rotation about one of these axes (indicated by i, , 2, , 6) is represented in the eigenvector of that mode. It is defined as

where defines the magnitude of the rigid body response of a degree of freedom in the model (N) to imposed rigid body motion (displacement or infinitesimal rotation) in the i-direction. For example, at a node with the usual three displacement and three rotation components, is where is unity; and all other zero, x, y, and z are the coordinates of the node; and , , and represent the coordinates of the center of rotation. The participation factors are, thus, defined for the translational degrees of freedom and for rotation around the center of rotation.

For coupled acoustic-structural eigenfrequency analyses, an additional acoustic participation factor is computed for each mode as outlined in “Coupled acoustic-structural medium analysis,” Section 2.9.1.

The effective mass for mode associated with kinematic direction i (, 2, , 6) is defined as

If the effective masses of all modes are added in any particular direction, the sum should give the total mass of the model, except for mass at kinematically restrained degrees of freedom. Thus, if the effective masses of the modes used in the analysis add up to a value that is significantly less than the model's total mass, this suggests that modes that have significant participation in excitation in that direction have not been extracted.

For coupled acoustic-structural eigenfrequency analyses, an additional acoustic effective mass is computed for each mode as outlined in “Coupled acoustic-structural medium analysis,” Section 2.9.1.

ABAQUS/Standard provides an option to define a composite damping factor for each material. These are assembled into fractions of critical damping values for each mode, , according to

where is the critical damping fraction given for material a and is the part of the structure's mass matrix made up of material a.