
We now discuss how to account for nonlinearity in an ABAQUS analysis. The main focus is on geometric nonlinearity.

Incorporating the effects of geometric nonlinearity in an analysis requires only minor changes to the input file. You need to add the NLGEOM parameter to the *STEP option and remove the PERTURBATION parameter. You may also add the INC parameter to specify the maximum number of increments allowed during the step. ABAQUS terminates the analysis with an error message if it needs more increments than this limit to complete the step. The default number of increments for a step is 100; if significant nonlinearity is present in the simulation, the analysis may require many more increments. The INC parameter specifies an upper limit on the number of increments that ABAQUS can use, rather than the number of increments it must use. For example, a step involving nonlinear geometry with a maximum of 25 increments would be specified as:
*STEP, NLGEOM, INC=25
In a nonlinear analysis a step takes place over a finite period of “time,” although this “time” has no physical meaning unless inertial effects or rate-dependent behavior are important. The data line on the procedure option used in the step specifies the initial time increment and the total time for the step. For example,
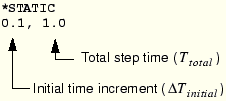
![]()
Although you must specify the initial increment size, ABAQUS automatically controls the size of the subsequent increments. This automatic control of the increment size is suitable for the majority of nonlinear simulations performed with ABAQUS, although further controls on the increment size are available. ABAQUS will terminate an analysis if excessive cutbacks caused by convergence problems reduce the increment size below the minimum value. The default minimum allowable time increment, ![]() , is 10–5 times the total step time. By default, ABAQUS has no upper limit on the increment size,
, is 10–5 times the total step time. By default, ABAQUS has no upper limit on the increment size, ![]() , other than the total step time. Depending on your ABAQUS simulation, you may want to specify different minimum and/or maximum allowable increment sizes. For example, if you know that your simulation may have trouble obtaining a solution if too large a load increment is applied, perhaps because the model may undergo plastic deformation, you may want to decrease
, other than the total step time. Depending on your ABAQUS simulation, you may want to specify different minimum and/or maximum allowable increment sizes. For example, if you know that your simulation may have trouble obtaining a solution if too large a load increment is applied, perhaps because the model may undergo plastic deformation, you may want to decrease ![]() .
.
The following input describes a static analysis in which the load is applied over 5 units of time and the initial time increment is 1 unit of time; the minimum and maximum time increments are set to 0.0001 and 1.5, respectively:
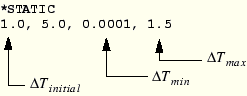
Local directions
In a geometrically nonlinear analysis the local material directions may rotate with the deformation in each element. For shell, beam, and truss elements the local material directions always rotate with the deformation. For solid elements the local material directions rotate with the deformation only if the elements refer to an *ORIENTATION option; otherwise, the local material directions remain constant throughout the analysis.
Local directions defined at nodes by using the *TRANSFORM option remain fixed throughout the analysis; they do not rotate with the deformation. See “Transformed coordinate systems,” Section 2.1.5 of the ABAQUS Analysis User's Manual, for further details.
Effect on subsequent steps
Once you include the NLGEOM parameter on the *STEP option, geometric nonlinearity is considered in all subsequent steps. If the NLGEOM parameter is omitted in a subsequent step, ABAQUS will issue a warning stating that nonlinear geometric effects are being included in the step anyway.
Other geometrically nonlinear effects
The large deformations in a model are not the only important nonlinear geometric effects that are considered when the NLGEOM parameter is used. Using this parameter also causes ABAQUS to include terms in the element stiffness calculations that are caused by the applied loads, the so-called load stiffness. These terms improve convergence behavior. In addition, the membrane loads in shells and the axial loads in cables and beams contribute much of the stiffness of these structures in response to transverse loads. By including geometric nonlinearity, the membrane stiffness in response to transverse loads is considered as well.

The addition of material nonlinearity to ABAQUS input files is discussed in Chapter 8, “Materials.”

The introduction of boundary nonlinearity is discussed in Chapter 11, “Contact.”