Product: ABAQUS/Standard
In this section the general analysis procedures for elements that include piezoelectric coupling are discussed.
The transient dynamic analysis capability for elements that include piezoelectric coupling is illustrated. Both concentrated nodal electrical charges and potentials are applied in separate analyses.
A piezoelectric bar [1 × 1 × 10] is subjected to an electrical potential. The potentials on the longitudinal top surface are prescribed to 1, and the potentials on the longitudinal bottom surface are prescribed to 0. The electrodes are simulated by using equations that set all the potentials on a face to the same prescribed value. The material is polarized in the local 3-direction.
The block is modeled using five C3D8E elements along the length. The material properties for the PZT-5H material that is used in the tests are as follows:
Elasticity properties:
Piezoelectric coupling matrix (strain coefficients):
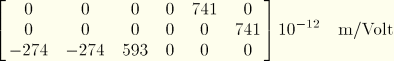
Dielectric matrix for fully constrained material:
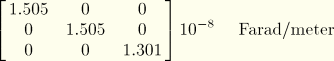
The piezoelectric coefficient matrix 
and the dielectric matrix 
for an unconstrained material, which are commonly used electrical properties in the piezoelectric literature, can be expressed in terms of the piezoelectrical properties mentioned above. These relationships are given in “Piezoelectric analysis,” Section 2.10.1 of the ABAQUS Theory Manual. These properties are commonly provided by the manufacturer. For the PZT-5H material the properties are as follows:
Piezoelectric coefficient matrix :
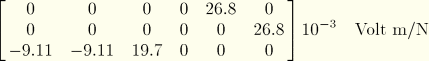
Dielectric matrix for an unconstrained material :
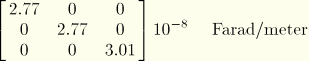
The tests involve a transient dynamic step in which the potential on the top surface is ramped up to 1 Volt in 0.014 seconds and then held constant for the remainder of the step. The results at the end of the step correspond to the static solution.
The applied electrical potential of 1 Volt results in a potential gradient of 1 Volt/m. The piezoelectric constants 
and 
can be used to estimate the electrical charge per unit area. In the case of an unconstrained material
is the potential gradient and 
is the charge density in the local 3-direction. So the charge density is equal to 
= 3.01 × 10–8. The area to which the voltage is applied is 10; therefore, the static reaction charge should be about 3.01 × 10–7. The results of ppzodyn1.inp confirm this reaction charge. In the input file ppzodyn2.inp a concentrated nodal electrical charge of 3.01 × 10–7 is applied instead of a potential value of 1 at the top surface. This results in a potential of 1 Volt on the top surface.Dynamic analysis with prescribed potentials.
Dynamic analysis with concentrated nodal electrical charges.
The geometrically nonlinear static analysis capability for a piezoelectric material is illustrated. A beam clamped at both ends is subjected to a potential that results in a loading that reaches the critical buckling load.
A beam of piezoelectric material is clamped at both sides and is subjected to an electrical potential. The beam is 0.4 m long with a width of 0.006 m and a thickness of 0.005 m. The potentials at one end of the beam are prescribed to 500 kVolts, and the potentials at the other end are prescribed to 0 kVolt. The electrodes are simulated by using equations that set the potential of all the nodes at each end of the beam to the same prescribed value. In the first step a small load is applied to the center to induce a small geometric imperfection.
The block is modeled using 20 C3D20E elements. The material properties for PZT-5H, which is used for the simulation, are given in the previous section.
The critical buckling load for the beam is
is the Young's modulus in the longitudinal direction and 
is the appropriate moment of inertia for the beam section. The analysis shows a critical compressive force of 773 N. The compressive force converges to the analytical buckling load with mesh refinement.Five blocks modeled with different piezoelectric element types are subjected to an electrical potential. The potentials at one side are prescribed to 1 Volt, and the potentials at the opposite side are prescribed to 0 Volt. The blocks are tied to three orthogonal surfaces to prevent unconstrained rigid body motions but are free to move tangentially with respect to the surfaces. The surfaces are also used to prescribe the rigid body rotations.
A block of PZT-5H is subjected to different loadings from which the piezoelectric material properties can be validated.
In the first step the potentials at the two opposite sides in the local 3-direction of the material are prescribed. Sufficient boundary conditions are applied to prevent rigid body motions, but the model is otherwise unconstrained. The piezoelectric constants = 593 × 10–12 and = 19.7 × 10–3 can be expressed in terms of the strain 
, the potential gradient , and the charge density as
, 
, , 
, 
, and are verified by using the numerically obtained values of the strains 
, 
, and . The dielectric constant 
in the local 3-direction for an unconstrained material is given by
and confirm the above relationships. In Steps 2–4 the model is charged in different ways verifying the same piezoelectrical material parameters as in Step 1. In Step 2 the potentials of the bottom and the top surface are switched. In Step 3 a nodal concentrated electrical charge is applied, and in Step 4 a distributed electrical charge is applied instead of prescribing the potentials. In Step 5 a potential gradient is applied in the local 1-direction to verify the piezoelectric properties 
, 
, and 
. In Steps 6–7 an open circuit condition is applied (the potential gradient is not prescribed by voltage boundary conditions), which results in reaction charges that are equal to zero. The piezoelectric constitutive equations can be written in different forms. In particular, the strain can be expressed in terms of either the potential gradient 
or the charge density 
. If the constitutive relation is expressed in terms of the potential gradient, the compliance data (typically denoted as 
in the piezoelectric literature) define the mechanical behavior at zero potential gradient. In ABAQUS the stiffness data at zero potential gradient are used to specify the mechanical behavior. If the constitutive relation is expressed using the charge density, the compliance matrix (typically denoted as 
in the piezoelectric literature) defines the mechanical behavior at zero charge density. The compliance can be obtained from the compliance and the electrical properties. For the PZT-5H material, 
= 14.05 × 10–12, 
= –7.27 × 10–12, 
= –3.05 × 10–12, 
= –3.05 × 10–12, and 
= 8.99 × 10–12. By loading the model at zero charge (in open circuit condition), these elastic compliances are verified.
Geometrically linear static analysis used to validate piezoelectric material properties.
Geometrically nonlinear static analysis used to validate piezoelectric material properties.
Geometrically nonlinear static analysis used to validate temperature- and field-variable-dependent piezoelectric material properties.
