3.5.2 Beam element formulation

Products: ABAQUS/Standard ABAQUS/Explicit
At a given stage in the deformation history of the beam, the position of a material point in the cross-section is given by the expression
In this expression
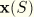
is the position of a point on the centerline,
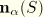
are unit orthogonal direction vectors in the plane of the beam section,
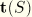
is the unit vector orthogonal to
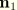
and
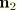
,
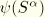
is the warping function of the section,
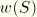
is the warping amplitude, and
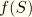
is a cross-sectional scaling factor depending on the stretch of the beam.
These quantities are functions of the beam axis coordinate 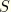 and the cross-sectional coordinates
and the cross-sectional coordinates 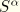 , which are assumed to be distances measured in the original (reference) configuration of the beam. The warping function is chosen such that the value at the origin of the section vanishes:
, which are assumed to be distances measured in the original (reference) configuration of the beam. The warping function is chosen such that the value at the origin of the section vanishes: 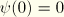 .
.
It is assumed that at the integration points along the beam, the beam section directions are approximately orthogonal to the beam axis tangent  given by
given by
where

is the axial stretch given by
The normality condition is enforced numerically by penalizing the transverse shear strains
This condition is assumed to be satisfied exactly in the original configuration.
In what follows, 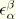 is the alternator
is the alternator
The curvature of the beam is defined by
and the twist of the beam follows from
The “bicurvature” of the beam is defined by
The bicurvature defines the axial strain variation in the section due to the twist of the beam. The expression for the curvature and the twist can be combined to yield
Before we derive strain measures from these expressions, we will consider in detail how the above quantities and their first and second variations are obtained for a typical beam finite element.
Beam element in undeformed configuration

In the undeformed configuration, we use capital letters for all quantities. We assume that the undeformed state has no warping, so the position of a material point is given by
and the curvatures and twist are defined by
where
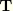
is the unit vector orthogonal to
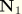
and
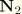
; i.e.,
We assume that the section normal
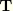
coincides with the beam tangent
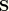
.
In the element the position of a point on the axis is interpolated from nodal positions 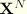 with standard interpolation functions as
with standard interpolation functions as
where
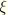
is a parametric coordinate, typically varying between
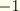
and

along the element. The beam axis tangent is readily computed as
The section normals are interpolated from user-defined nodal normals
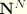
. However, we cannot use a simple interpolation since this would not create integration point normals orthogonal to the beam tangent
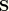
. Hence, we use a two-step approach. First, we create approximate normals by the interpolation
Then, we orthonormalize these vectors with respect to
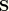
by
and subsequently, with respect to each other by
where it has been assumed that

and
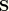
form a right-handed system. This provides
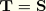
.
The curvature and the twist in the initial configuration are calculated directly from  as
as
The “average” twist is taken, since, in general,
The gradient of the normal vectors is then obtained as
and, therefore, the curvature and twist are also equal to
The procedure followed above to derive
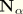
and
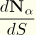
is not unique but provides values that satisfy the proper orthonormality conditions. This procedure is followed only for the undeformed configuration. For subsequent configurations
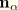
and
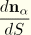
are obtained individually by forward integration of the kinematic equations.
Change of position, warping, and normal direction

We assume that the position of the beam axis and the orientation of the normals can undergo (independent) changes. The change in position of the axis is described by the velocity vector 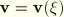 , which can be obtained from nodal velocities
, which can be obtained from nodal velocities 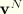 with the standard interpolation functions as
with the standard interpolation functions as
The change in orientation of the normals is described by the spin vector

, which is obtained from nodal spin vectors
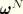
with the same interpolation functions
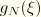
, as
Rigid body motion is included since the original position
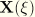
is obtained by the same interpolation as
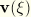
. The rate of change of warping is also defined in terms of the rate of change of nodal warping
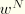
with the standard interpolation functions as
The velocity and spin describe the
rate of change of the position and orientation.
Finite changes in position are obtained by integration of the velocities over a finite time increment as
Similarly, for the warping,
The spin is related to the rate of change of the rotation quaternion
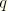
by
where
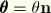
is the total or Euler rotation.
The relation between spin and quaternion can be integrated exactly if it is assumed that the spin is constant over the time increment 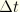 . We then define
. We then define
and the incremental rotation quaternion follows from
This allows us to update the normal directions at the nodes and at stress points with
In this equation we use the notation that
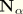
is
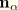
at the beginning of the current increment; i.e.,
For the entire motion the new normal directions can be formally expressed as
where
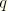
is defined by the product rule
Here
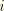
is an increment and
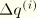
is the rotation quaternion for that increment. The section normal
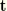
is updated the same way.
Change of curvature and twist

The curvature and the twist involve the derivative of the normal vector with respect to 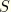 . From the update rule for
. From the update rule for 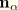 ,
,
The second term can be written as
Hence, the scalar parts of the first two terms cancel each other, and the vector parts are the same. Therefore,
Because
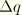
is a rotation quaternion, its inverse is equal to its conjugate (
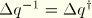
), and, hence, we can write
where
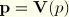
denotes the vector part of a quaternion. For the first term we use the relation
This leads to
which is a vector. From the definitions of
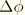
and
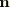
it follows that
These results provide
We see that
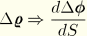
if
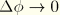
.
For the second term we express 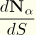 in terms of the curvature and twist at the beginning of the increment, which yields
in terms of the curvature and twist at the beginning of the increment, which yields
Combining these terms,
The current curvature and twist are, therefore,
and
Hence, the current curvature and twist are updated by a summation over all increments as given by
First variations

The first variations of the geometric quantities are readily obtained. Recall that
It follows that
where in the expression for
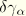
we have assumed that
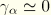
and
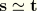
. For the variations in the curvature and twist, we note that
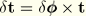
. Hence, it follows that
These terms will be used in the virtual work equation that will be discussed later. In using the above expressions the rotational quantities are obtained by interpolation from nodal variational quantities that are assumed to be valid for the velocity fields as
Solution with Newton's algorithm

Newton's algorithm involves linearization of the incremental equations. The equations must be linearized around the current (latest) state. At the integration points these equations simply take the form
The corrections
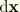
and
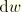
are readily obtained from the nodal corrections with the interpolation functions
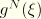
as
The corrections
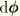
are defined with respect to the end of the increment: we call such corrections “compound” corrections. However, it has been assumed that the total incremental rotation
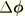
would be interpolated with
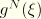
as
Linearization of this equation yields
where

are corrections in
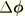
in an additive sense such that
To relate the additive correction

to the compound correction
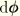
, we use the formula obtained for
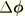
to find
Similarly, at the nodes we find
Now we assume that the difference in incremental rotation along a beam element is small; i.e.,
which implies that either
or
In the first case we can use the approximations
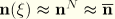
and

which, with the use of the interpolation functions for

, gives
In the second case it follows directly that
In either case
This approximate relationship is used only in the creation of the Jacobian, so the approximation will at worst result in reduced speed of convergence.
Once a nodal update vector 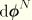 is obtained, an exact update procedure is followed. This is achieved by a transformation into quaternions, use of exact quaternion update formula, and transformation of the results back into an incremental Euler rotation vector:
is obtained, an exact update procedure is followed. This is achieved by a transformation into quaternions, use of exact quaternion update formula, and transformation of the results back into an incremental Euler rotation vector:
The incremental rotation vector at the integration point is obtained by interpolation. Subsequently, we can calculate the updated integration point normals and the incremental curvature and twist.
Second variations

For the calculation of the Jacobian, we also need the second variation in the generalized quantities. These follow from the first variations:
where we have again used
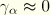
.
For the second variation of the curvature we find
Rewriting the second and third terms and combining the others yields
The second variation of twist is
Then, following the same procedure as for
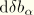
,
Finally, we note
The resulting second variations are summarized as
Strains

The gradient of the current position of a point in the section with respect to the coordinate 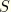 is
is
We will keep only terms up to order
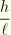
. We assume that
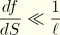
, and—hence—the second term can be neglected. We also assume that
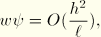
and—since
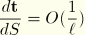
—we can neglect the last term as well. However, the warping function may vary rapidly near the ends where warping is constrained. Hence,
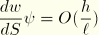
and should be preserved. With those approximations,
The gradients with respect to
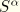
are
Correspondingly, in the original configuration
The above relations are readily inverted to yield
The deformation gradient then becomes
We define the initial length ratio R as
In the expression enclosed within square brackets above, terms of order
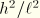
can again be neglected. However, it is assumed that the section may have low resistance to torsion and that, hence, the warping and twist may be large. This is particularly true for thin walled open sections. Hence, we obtain:
We calculate the components of
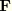
in a corotational system with the approximation
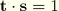
. This provides
We again neglect all terms of order
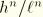
for
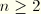
, except the term involving
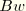
. The equations then simplify to
Consistent with traditional shell and beam theories, we slightly adapt the term involving the initial curvature
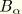
—instead of multiplying it with

, we multiply it with

. Such a change does not significantly increase the error in the curvature calculation, since we do not properly account for the initial curvature in the volume integration anyway. Hence, we find for

:
We now make a multiplicative decomposition of
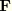
into a “stretch” part

and a “distortion” part
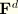
such that
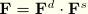
.
For  we choose
we choose
and, hence,
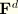
is
Since

is a diagonal tensor, the logarithmic “stretch” strains are immediately available as
Since the “distortional” strains are small, we obtain them from
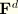
with the Green-Lagrange formula:
For the components this yields
Note that these strains are small. Since the various terms have different dependence on the cross-sectional coordinates, this leads to the conditions
The last condition will generally require that both
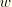
and
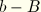
are small, since
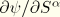
will not be proportional to
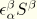
. However, for thin walled open section beams the proportionality is approximately satisfied and, therefore, we obtain in that case
Note that within the desired accuracy this equation even holds for other sections: in that case both the right-hand and left-hand side are very small. Substitution in the expression for the Green-Lagrange strain yields the (small) distortional strains:
The total strains are obtained simply by addition as
We assume that there are no stresses in the
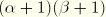
directions. Hence, the strains in these directions do not contribute to virtual work and do not need to be considered any further.
It is useful to split the total warping 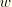 in two parts: a part due to “free” warping
in two parts: a part due to “free” warping 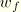 minus a part due to warping prevention
minus a part due to warping prevention 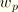 :
: 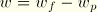 . We assume that the warping function
. We assume that the warping function  is chosen such that the free warping is related to the twist with the relation
is chosen such that the free warping is related to the twist with the relation
This makes it possible to write the expression for
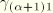
as
It is desirable to choose the cross-sectional resultants such that they are completely uncoupled. In addition, we assume that the axial strain variation across the section due to the second-order term in the twist is not significant. Therefore, we consider only the
average axial strain due to the second-order twist term. Hence, we introduce the average axial strain
where
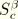
are the coordinates of the centroid,
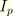
is the polar moment of inertia, and
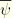
is the average value of the warping function:
Similarly, we introduce the average shear strain
This last expression can be simplified by the introduction of the shear center coordinates 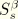 , which are related to the warping function by
, which are related to the warping function by
This yields
Note that the average value is in fact the value at the shear center if warping prevention is absent (
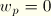
). However, for full warping prevention (
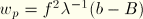
) the average value corresponds to the value obtained at the centroid.
Instead of the original warping function 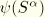 we now introduce a modified warping function
we now introduce a modified warping function 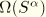 related to
related to  by
by
This function in fact represents the classical definition of a warping function with an area weighted average of zero. The average value
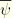
can be obtained from the classical warping function with the condition that
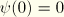
:
The expression for the average axial strain then becomes
and the location of the shear center is
The strains can, thus, be written in the form
The second term in the expression for
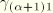
is proportional to the shear strain field for pure elastic torsion:
We use this definition to eliminate the gradient of
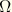
from the expression for the shear strain, which yields as final expression for the strains
Virtual work

Since it was assumed that there are no stresses in the 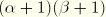 directions, the virtual work contribution is
directions, the virtual work contribution is
The strain variations are obtained by linearization of the expressions for the strains
where all terms of the order of the “distortional” strains have been neglected. From the expressions for the average axial strain and average shear strain, we obtain the average axial and shear strain variations as
where
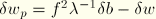
and again all terms of the order of the “distortional” strains have been neglected.
We now introduce the generalized section forces as defined below:
which transforms the virtual work contribution into
Observe that the total torque
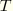
relative to the centroid of the section is the sum of the twisting moment and the warping moment:
The rate of change of virtual work

To obtain the rate of change of virtual work, we first transform the integrations in the virtual work equation to the original volume such that
The strain variations relative to the original state are then
The strain variations relative to the original state are
The rate of change of virtual work is then
where we have neglected terms of order
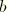
. The changes in stress follow from the constitutive law
We approximate
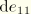
and
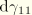
with the same relations as used for virtual work:
and for the average strain rates
We now neglect all terms that involve the product of a stress tensor; a variation in curvature, twist, or warping; and a change in axial strain of the cross-section. Using the previously obtained expressions for the second variations in
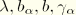
, and
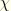
and transforming the results into the current state, this provides
The incremental moments, forces, etc. are defined as
For the determination of the initial stress stiffness, we assume that the second variations of the warping function and its derivative vanish:
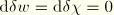
. Consequently,
and, therefore, only the torque relative to the centroid plays a role in the initial stress contribution to the rate of change of virtual work:
The second variations of
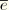
and
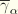
contain contributions of the second variation in curvature and twist. These can be separated out by defining the bending moments and the torque relative to the origin of the cross-sectional coordinate system:
The expression for the rate of change of virtual work then takes the form
We propose to make the “cross-section size” a function of the stretch

. For the thermal stretch of the section we use isotropic expansion
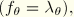
and for the “mechanical” stretch of the section we assume an effective Poisson's ratio
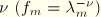
. The total cross-sectional stretch is
so that
Using this in the above expression for the rate of change of virtual work, we find
This expression is symmetric if the material tensor
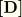
is symmetric.
Section integration

The formulation presented in the previous pages is valid for all possible beam types. However, different classes of beams will result in different final formulations. We consider three different classes of beams:
Beams in which warping may be constrained. These beams generally have an open, thin walled section reinforced with some relatively solid parts or some relatively small closed cells and have a torsional stiffness that is considerably smaller than the polar moment of inertia. Hence, in the elastic range, the warping can be large, and warping prevention at the ends can contribute significantly to the torsional rigidity of the beam. In this case both the torsional shear stresses and the axial warping stresses can be of the same order of magnitude as the stresses due to axial forces and bending moments, and the complete theory must be used.
Beams in which warping is unconstrained. These beams generally have a solid section or a closed, thin walled section and have a torsional stiffness that is of the same order of magnitude as the polar moment of inertia of the section. Hence, in the elastic range the warping is rather small, and it is assumed that warping prevention at the ends can be neglected. The axial warping stresses are assumed to be negligible, but the torsional shear stresses are assumed to be of the same order of magnitude as the stresses due to axial forces and bending moments. In this case the warping is dependent on the twist and can be eliminated as an independent variable, which leads to a considerably simplified formulation.
Beams in which warping constraints dominate the torsional rigidity. These beams generally have an open, thin walled section and have a torsional stiffness that is much smaller than the polar moment of inertia. In the elastic range the warping is likely to be large, and warping constraints are essential to provide torsional stiffness for the beam. In this case the axial stresses may be of the same order of magnitude as the stresses due to axial forces and bending moments, but the torsional shear stresses are relatively small. Hence, the warping can be coupled to the twist with a relatively stiff elastic constraint but cannot be eliminated because it must be possible to prevent warping at the nodes.
Examples of cross-sections for the last two classes will be derived after the general discussion of sections with and without warping prevention.
In ABAQUS we neglect the effect of shear stresses due to transverse shear forces at individual material points. We will consequently always assume elastic behavior of the section in transverse shear, leading to the relations
where
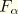
are the transverse shear forces, working at the shear center, and
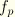
is the “slenderness compensation factor” used to prevent the shear stiffness from becoming too big in slender beams. The slenderness compensation factor is defined as
where
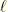
is the length of the element and
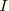
is the larger of the moments of inertia
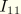
and
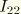
. Hence, the transverse shear terms do not need to be considered in any further detail.
The fact that the transverse shear forces are considered separately allows us to write
where
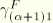
and
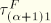
are the strains and stresses due to transverse shear forces and
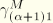
and
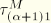
are the strains and stresses due to a twisting around the shear center. Substitution in the expressions for the twisting and warping moments yields
where we used the fact that
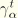
was calculated based on application of a twisting moment around the shear center and, hence, does not do any work on the shear stresses due to transverse shear forces.
The warping function 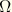 is assumed to be determined based on isotropic, homogeneous elastic behavior of the section in shear. For this case the elastic energy due to twist is
is assumed to be determined based on isotropic, homogeneous elastic behavior of the section in shear. For this case the elastic energy due to twist is
For twist without warping constraints
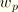
vanishes and the energy per unit length of the beam is
where we have introduced the torsion integral

given by
With complete warping prevention the
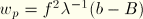
and the energy per unit length of the beam is
where we have introduced the polar moment of inertia
For unconstrained warping 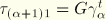 . Since the twisting moment must be equal to
. Since the twisting moment must be equal to
and since
it follows that
Beams with unconstrained warping

For this beam type, warping prevention is not taken into consideration. Hence we assume 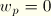 . In addition we assume that axial strains due to warping can be neglected:
. In addition we assume that axial strains due to warping can be neglected: 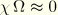 .
.
For the strains at a material point this yields
and for the variations in the strains
Substitution in the virtual work statement yields
where the expressions derived earlier for

,
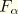
,
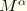
, and
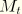
apply.
Although there is no warping prevention in the section, the warping moment 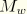 does not vanish. From the expression obtained earlier follows
does not vanish. From the expression obtained earlier follows
This yields for the torque around the centroid
and for the torque around the origin
For the rate of change of virtual work we obtain
Beams with elastic torsion and constrained warping

Consider the case that the shear stresses are defined from the shear strains by linear elastic response, with a constant shear modulus 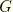 :
:
This allows us to write for the twisting and warping moments:
Substitution of these expressions in the part of the virtual work equation related to torsion yields
Note that the torque
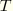
around the centroid is
Hence, we can write virtual work in terms of the primary variables
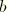
and
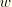
:
The complete virtual work equation has the form
where

,
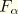
,
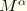
and
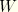
are defined as before.
For the rate of change of virtual work we obtain similarly
with
We now discuss some specific section types incorporated in ABAQUS.
Circular section

For this type of section, warping is absent. Hence,
Solid noncircular sections

Solid sections such as rectangles or trapezoids are included in this category. The warping function  is a harmonic function and is subject to the condition that no shear stress component can act normal to the boundary of the cross-section. Although it is possible to determine the warping function
is a harmonic function and is subject to the condition that no shear stress component can act normal to the boundary of the cross-section. Although it is possible to determine the warping function  in this manner, we choose to work in terms of the Saint-Venant's stress function because of its simplicity. Following standard procedures we normalize this function so that the (elastic) shear strains can be derived directly from it. We introduce the function
in this manner, we choose to work in terms of the Saint-Venant's stress function because of its simplicity. Following standard procedures we normalize this function so that the (elastic) shear strains can be derived directly from it. We introduce the function 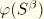 , which is differentiable in the cross-section and has the property that
, which is differentiable in the cross-section and has the property that
The stress function is determined by solving the differential equation of the form
where
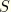
represents the boundary of the section. This boundary condition ensures that no shear stress component can act normal to the boundary.
For the solid noncircular sections this differential equation is solved numerically using a second-order isoparametric finite element. The torsional constant of the bar is then equal to twice the volume under the normalized stress function surface.
Closed, thin walled cross-sections

In this case we assume that the shear strain perpendicular to the section must vanish so that
Since
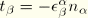
, this yields
which can be identically satisfied anywhere. The normalized shear strain along the section is
where

is the distance along the section. Integrating this around the circumference yields
where
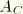
is the area enclosed by the section. With the assumption that the shear modulus is constant along the section, the total torsional elastic strain energy is
where
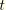
is the wall thickness. Minimization of the energy with the constraint enforced with a Lagrange multiplier
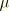
yields
Hence,
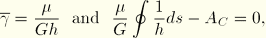
which combine to define
This allows calculation of
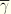
at any point in the section based on the section geometry.
Thin walled open sections

The most important sections that exhibit substantial warping are the thin walled open sections. For a single branch section we can conveniently express 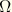 as a function of the coordinate
as a function of the coordinate  along the section and the coordinate
along the section and the coordinate  perpendicular to the section. A suitable approximation for
perpendicular to the section. A suitable approximation for 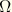 is
is
where

is the value at the centerline of the wall. Minimization of the torsional elastic energy yields
We now introduce
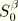
, which is the position of the middle of the wall. With
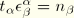
and
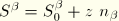
, and after carrying out the integration over

, the minimization condition simplifies to
Clearly, the dominant terms are of order
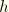
. This yields the equations
so that
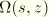
is
where
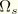
is the value of
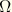
at the start of the integration over the section. Observe that
represents the
sectorial area between two points on the midsection relative to the shear center. Therefore, it readily follows that
so there is no coupling between twist and bending in the section for linear elastic material behavior. As was discussed before,
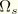
must be chosen such that
which eliminates the coupling between twist and axial extension in the section for linear elasticity.
Note that coupling terms still exist but that they are incorporated in the generalized strain displacement relations. The coupling between twist and extension is governed by 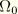 , the value of the warping function at the origin of the cross-sectional coordinate system. If the origin is on the section, this value can be evaluated properly. If the origin is not on the section (which means that the node is not connected to the section), we assume that
, the value of the warping function at the origin of the cross-sectional coordinate system. If the origin is on the section, this value can be evaluated properly. If the origin is not on the section (which means that the node is not connected to the section), we assume that  .
.
The torsion integral  is readily obtained as
is readily obtained as
and the polar moment of inertia is given by the expression
The above derivations cover single branch open sections. Multibranch open sections can be transformed into single branch open sections by connecting the end of one branch with the beginning of the next branch with a section that has thickness
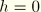
. Such dummy sections do not yield any contribution to the area, the moments of inertia, or the torsion integral and, hence, have no influence on the results.

![]()
![]() and the cross-sectional coordinates
and the cross-sectional coordinates ![]() , which are assumed to be distances measured in the original (reference) configuration of the beam. The warping function is chosen such that the value at the origin of the section vanishes:
, which are assumed to be distances measured in the original (reference) configuration of the beam. The warping function is chosen such that the value at the origin of the section vanishes: ![]() .
.![]() given by
given by ![]()
![]()
![]()
![]() is the alternator
is the alternator ![]()
![]()
![]()
![]()
![]()

![]()
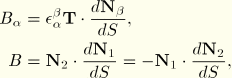
![]()
![]() with standard interpolation functions as
with standard interpolation functions as ![]()
![]()
![]()
![]()
![]()
![]() as
as 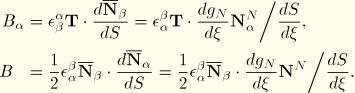
![]()
![]()
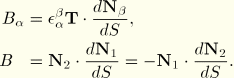

![]() , which can be obtained from nodal velocities
, which can be obtained from nodal velocities ![]() with the standard interpolation functions as
with the standard interpolation functions as ![]()
![]()
![]()
![]()
![]()
![]()
![]() . We then define
. We then define ![]()
![]()
![]()
![]()
![]()
![]()

![]() . From the update rule for
. From the update rule for ![]() ,
, ![]()
![]()
![]()
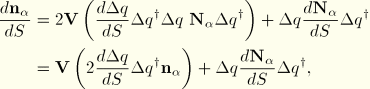
![]()
![]()
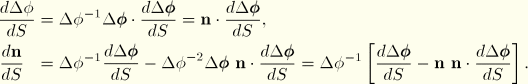
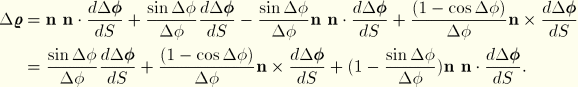
![]() in terms of the curvature and twist at the beginning of the increment, which yields
in terms of the curvature and twist at the beginning of the increment, which yields ![]()
![]()
![]()
![]()


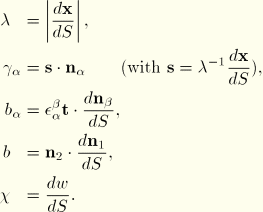

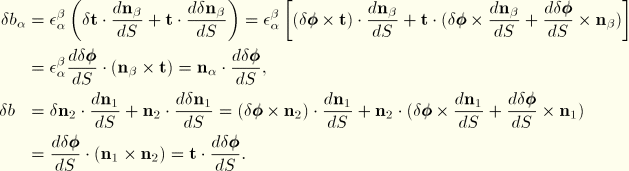
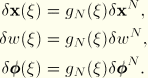

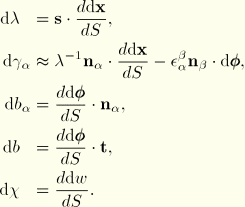
![]()
![]()
![]()
![]()
![]()
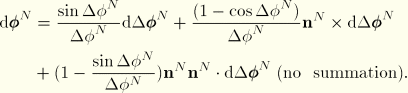
![]()
![]()
![]()
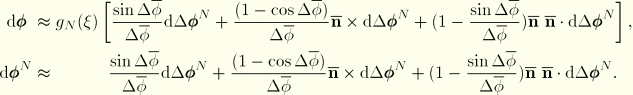
![]()
![]()
![]() is obtained, an exact update procedure is followed. This is achieved by a transformation into quaternions, use of exact quaternion update formula, and transformation of the results back into an incremental Euler rotation vector:
is obtained, an exact update procedure is followed. This is achieved by a transformation into quaternions, use of exact quaternion update formula, and transformation of the results back into an incremental Euler rotation vector: 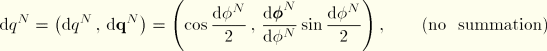
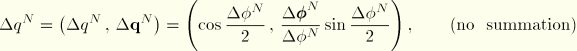
![]()
![]()

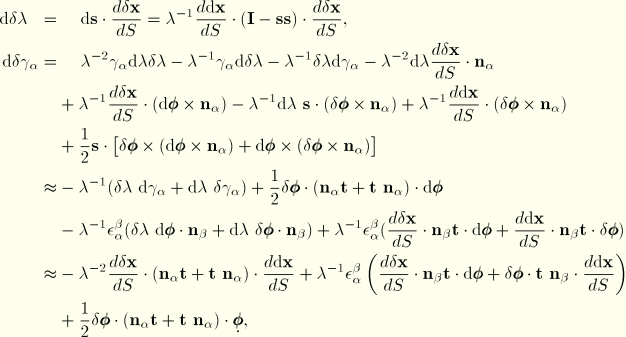
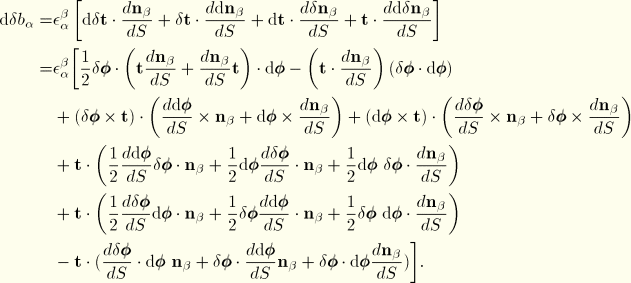
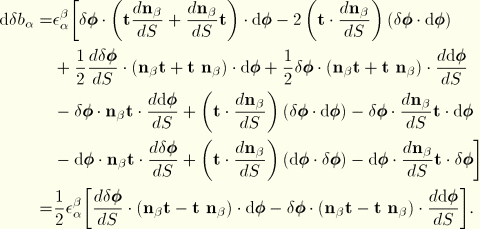
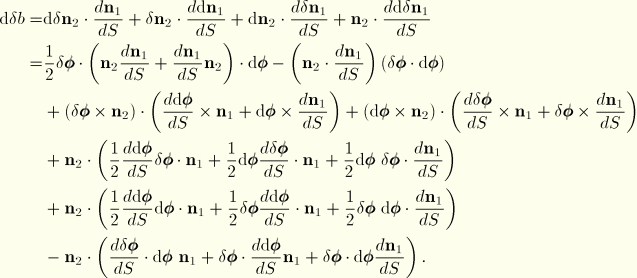
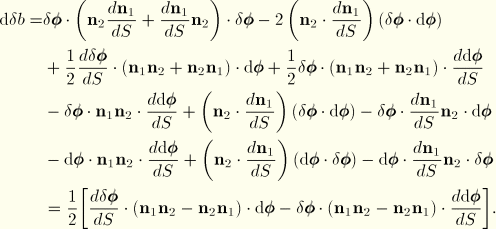
![]()
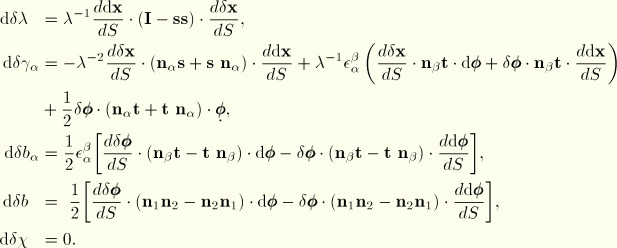

![]() is
is![]()
![]()
![]()
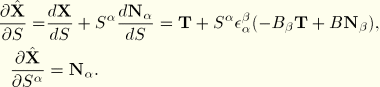
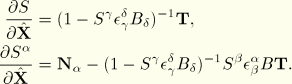
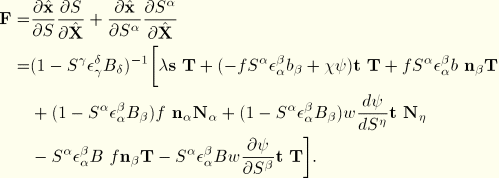
![]()
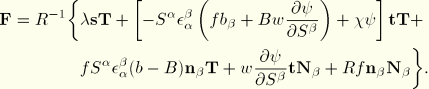
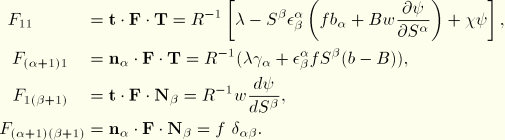
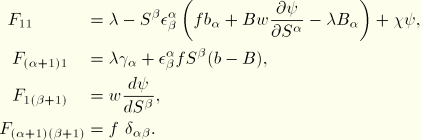
![]()
![]() we choose
we choose ![]()

![]()
![]()
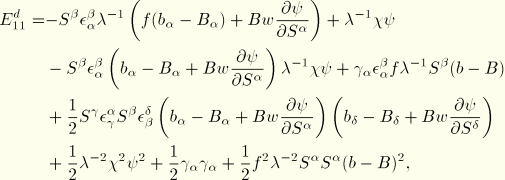
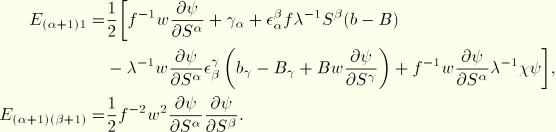
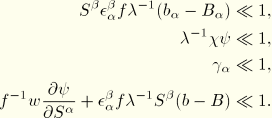
![]()
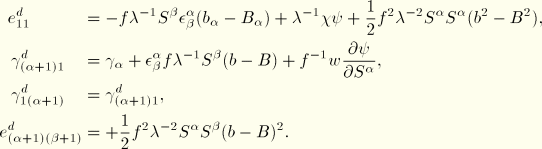
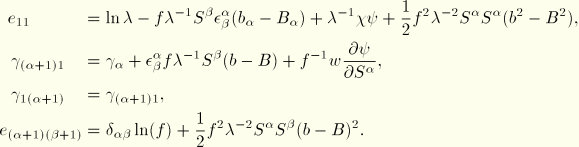
![]() in two parts: a part due to “free” warping
in two parts: a part due to “free” warping ![]() minus a part due to warping prevention
minus a part due to warping prevention ![]() :
: ![]() . We assume that the warping function
. We assume that the warping function ![]() is chosen such that the free warping is related to the twist with the relation
is chosen such that the free warping is related to the twist with the relation ![]()
![]()
![]()
![]()
![]()
![]() , which are related to the warping function by
, which are related to the warping function by ![]()
![]()
![]() we now introduce a modified warping function
we now introduce a modified warping function ![]() related to
related to ![]() by
by ![]()
![]()
![]()
![]()
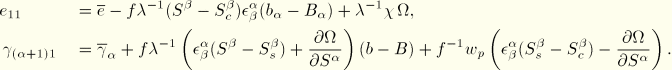
![]()
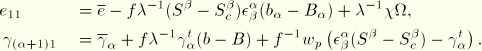

![]() directions, the virtual work contribution is
directions, the virtual work contribution is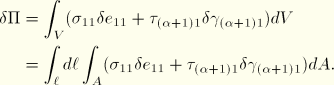
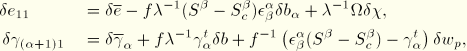
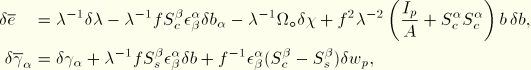
![]()
![]()

![]()
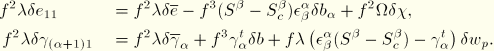
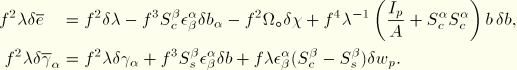
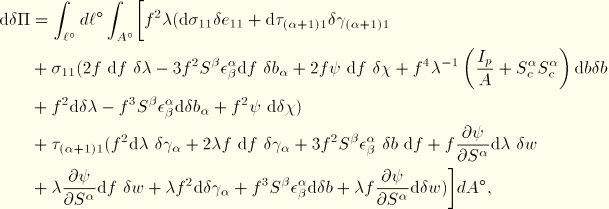
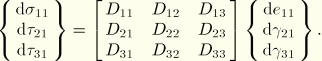
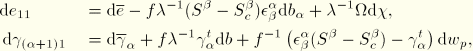
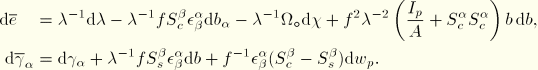
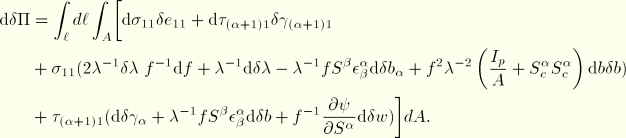
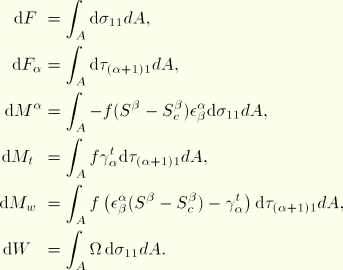
![]()
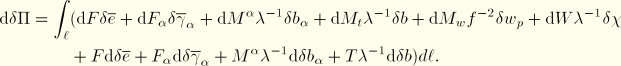
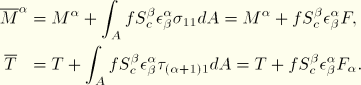
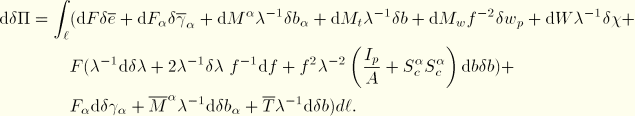
![]()
![]()
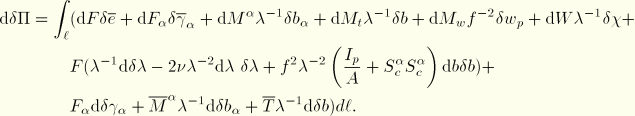

![]()
![]()
![]()
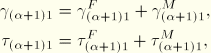
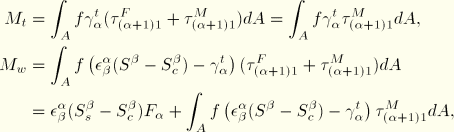
![]() is assumed to be determined based on isotropic, homogeneous elastic behavior of the section in shear. For this case the elastic energy due to twist is
is assumed to be determined based on isotropic, homogeneous elastic behavior of the section in shear. For this case the elastic energy due to twist is ![]()
![]()
![]()
![]()
![]()
![]() . Since the twisting moment must be equal to
. Since the twisting moment must be equal to ![]()
![]()
![]()

![]() . In addition we assume that axial strains due to warping can be neglected:
. In addition we assume that axial strains due to warping can be neglected: ![]() .
.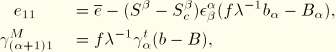
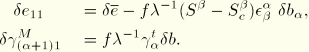
![]()
![]() does not vanish. From the expression obtained earlier follows
does not vanish. From the expression obtained earlier follows ![]()
![]()
![]()
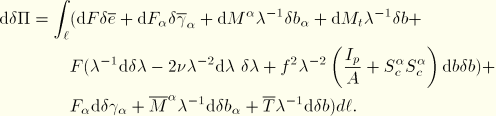

![]() :
: ![]()
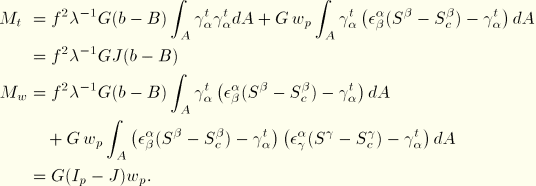
![]()
![]()
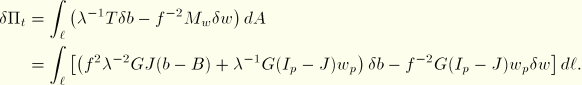
![]()
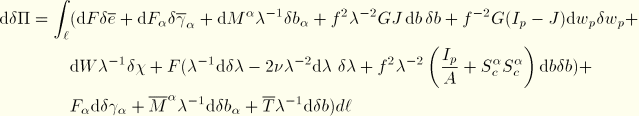
![]()

![]() is a harmonic function and is subject to the condition that no shear stress component can act normal to the boundary of the cross-section. Although it is possible to determine the warping function
is a harmonic function and is subject to the condition that no shear stress component can act normal to the boundary of the cross-section. Although it is possible to determine the warping function ![]() in this manner, we choose to work in terms of the Saint-Venant's stress function because of its simplicity. Following standard procedures we normalize this function so that the (elastic) shear strains can be derived directly from it. We introduce the function
in this manner, we choose to work in terms of the Saint-Venant's stress function because of its simplicity. Following standard procedures we normalize this function so that the (elastic) shear strains can be derived directly from it. We introduce the function ![]() , which is differentiable in the cross-section and has the property that
, which is differentiable in the cross-section and has the property that ![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() as a function of the coordinate
as a function of the coordinate ![]() along the section and the coordinate
along the section and the coordinate ![]() perpendicular to the section. A suitable approximation for
perpendicular to the section. A suitable approximation for ![]() is
is ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , the value of the warping function at the origin of the cross-sectional coordinate system. If the origin is on the section, this value can be evaluated properly. If the origin is not on the section (which means that the node is not connected to the section), we assume that
, the value of the warping function at the origin of the cross-sectional coordinate system. If the origin is on the section, this value can be evaluated properly. If the origin is not on the section (which means that the node is not connected to the section), we assume that ![]() .
.![]() is readily obtained as
is readily obtained as 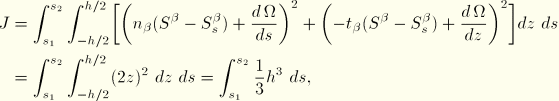
![]()