
The stability limit dictates the maximum time increment used by ABAQUS/Explicit. It is a critical factor in the performance of ABAQUS/Explicit. The following sections describe the stability limit and discuss how ABAQUS/Explicit determines this value. Issues surrounding the model design parameters that affect the stability limit are also addressed. These model parameters include the model mass, material, and mesh.

With the explicit method the state of the model is advanced through an increment of time, ![]() , based on the state of the model at the start of the increment at time
, based on the state of the model at the start of the increment at time ![]() . The amount of time that the state can be advanced and still remain an accurate representation of the problem is typically quite short. If the time increment is larger than this maximum amount of time, the increment is said to have exceeded the stability limit. A possible effect of exceeding the stability limit is a numerical instability, which may lead to an unbounded solution. It generally is not possible to determine the stability limit exactly, so conservative estimates are used instead. The stability limit has a great effect on reliability and accuracy, so it must be determined consistently and conservatively. For computational efficiency ABAQUS/Explicit chooses the time increments to be as close as possible to the stability limit without exceeding it.
. The amount of time that the state can be advanced and still remain an accurate representation of the problem is typically quite short. If the time increment is larger than this maximum amount of time, the increment is said to have exceeded the stability limit. A possible effect of exceeding the stability limit is a numerical instability, which may lead to an unbounded solution. It generally is not possible to determine the stability limit exactly, so conservative estimates are used instead. The stability limit has a great effect on reliability and accuracy, so it must be determined consistently and conservatively. For computational efficiency ABAQUS/Explicit chooses the time increments to be as close as possible to the stability limit without exceeding it.

The stability limit is defined in terms of the highest frequency in the system (![]() ). Without damping the stability limit is defined by the expression
). Without damping the stability limit is defined by the expression
![]()
![]()
The actual highest frequency in the system is based on a complex set of interacting factors, and it is not computationally feasible to calculate its exact value. Alternately, we use a simple estimate that is efficient and conservative. Instead of looking at the global model, we estimate the highest frequency of each individual element in the model, which is always associated with the dilatational mode. It can be shown that the highest element frequency determined on an element-by-element basis is always greater than or equal to the highest frequency in the assembled finite element model.
Based on the element-by-element estimate, the stability limit can be redefined using the element length, ![]() , and the wave speed of the material,
, and the wave speed of the material, ![]() :
:
![]()
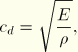
Our simplified stability limit definition provides some intuitive understanding. The stability limit is the transit time of a dilatational wave across the distance defined by the characteristic element length. If we know the size of the smallest element dimension and the wave speed of the material, we can estimate the stability limit. For example, if the smallest element dimension is 5 mm and the dilatational wave speed is 5000 m/s, the stable time increment is on the order of 1 × 10–6 s.

ABAQUS/Explicit uses equations such as those discussed in the previous section to adjust the time increment size throughout the analysis so that the stability limit, based on the current stage of the model, is never exceeded. Time incrementation is automatic and requires no user intervention, not even a suggested initial time increment. The stability limit is a mathematical concept resulting from the numerical model. Since the finite element program has all of the relevant details, it can determine an efficient and conservative stability limit. However, ABAQUS/Explicit does allow the user to override the automatic time incrementation, if desired. “Summary,” Section 3.9, briefly discusses manual time incrementation controls.

Since the mass density influences the stability limit, under some circumstances scaling the mass density can potentially increase the efficiency of an analysis. For example, because of the complex discretization of many models, there are often regions containing very small or poorly shaped elements that control the stability limit. These controlling elements are often few in number and may exist in localized areas. By increasing the mass of only these controlling elements, the stability limit can be increased significantly, while the effect on the overall dynamic behavior of the model may be negligible.
The automatic mass scaling features in ABAQUS/Explicit can keep offending elements from hindering the stability limit. There are two fundamental approaches used in mass scaling: defining a scaling factor directly or defining a desired element-by-element stable time increment for the elements whose mass is to be scaled. These two approaches, described in detail in the ABAQUS Analysis User's Manual, permit additional user control over the stability limit. However, use caution when employing mass scaling since significantly changing the mass of the model may change the physics of the problem.

The material model affects the stability limit through its effect on the dilatational wave speed. In a linear material the wave speed is constant; therefore, the only changes in the stability limit during the analysis result from changes in the smallest element dimension during the analysis. In a nonlinear material, such as a metal with plasticity, the wave speed changes as the material yields and the stiffness of the material changes. ABAQUS/Explicit monitors the effective wave speeds in the model throughout the analysis, and the current material state in each element is used for stability estimates. After yielding, the stiffness decreases, reducing the wave speed and, consequently, increasing the stability limit.

Since the stability limit is roughly proportional to the shortest element dimension, it is advantageous to keep the element size as large as possible. Unfortunately, for accurate analyses a fine mesh is often necessary. To obtain the highest possible stability limit while using the required level of mesh refinement, the best approach is to have a mesh that is as uniform as possible. Since the stability limit is based on the smallest element dimension in the model, even a single small or poorly shaped element can reduce the stability limit drastically. For diagnostic purposes ABAQUS/Explicit provides a list in the status (.sta) file of the 10 elements in the mesh with the lowest stability limit. If the model contains some elements whose stability limits are much lower than those of the rest of the mesh, remeshing the model more uniformly may be worthwhile.

ABAQUS/Explicit remains stable for most elements under most circumstances. It is possible, however, to define spring and dashpot elements such that they become unstable during the course of an analysis. Therefore, it is useful to be able to recognize a numerical instability if it occurs in your analysis. If it does occur, the result typically will be unbounded, nonphysical, and often oscillatory solutions. The examples at the end of this chapter use simple spring and dashpot problems to illustrate instabilities.